Drucker–Prager 屈服准则

Drucker–Prager 屈服准则主要用于岩土类材料研究，属于各向同性屈服准则

对于多孔金属、混凝土以及土壤和岩石等土木材料，塑性变形源于与压力相关的微观过程。相应的屈服条件不仅依赖于应力张量的偏差部分，还与静水部分密切相关

Drucker–Prager 屈服准则认为，当八面体截面上的剪切应力克服了材料的粘聚力和摩擦阻力时，材料开始屈服，即

\[ \tau_{\text{oct}} = \tau_f + \sqrt{\frac{2}{3}} k, \]

见 Mises 屈服准则 中的推导，和 Mohr–Coulomb 屈服准则 中的变量解释

其中，\(\tau_{\text{oct}} = \left( \frac{2}{3} J_2 \right)^{1/2},\ \tau_f = -\tan\phi\cdot \sigma_{\text{oct}} = -\tan\phi \cdot \frac{1}{3} I_1\)，\(k\) 是材料参数，与粘聚力相关。代入上式整理得到

\[ \sqrt{J_{2}} + \tan\phi \cdot \frac{\sqrt{6}}{6} I_1 - k = 0. \]

Drucker–Prager 屈服准则的一般形式写为

\[ \sqrt{J_{2}} + \alpha I_1 - k = 0. \]

\[ k = \frac{6c\cos\phi}{\sqrt{3}(3-\sin\phi)}. \]

几何意义

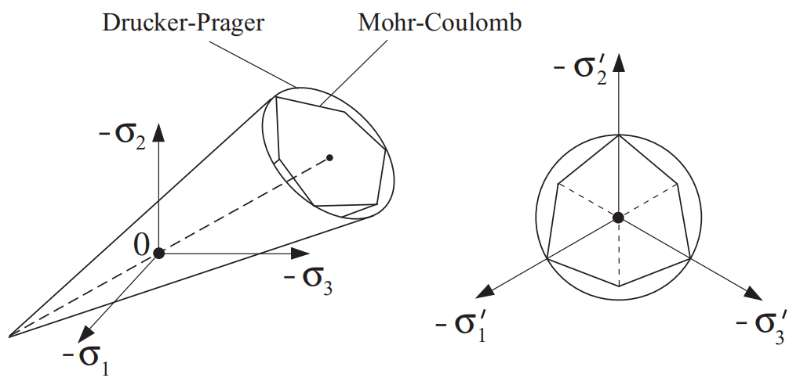
Fig. 43 Mohr–Coulomb 屈服准则和 Drucker–Prager 屈服准则