有限元计算基础#
在有限元方法中,偏微分方程通过变分法与分片多项式进行离散,最终被转化为线性/非线性方程组的形式。例如,对于一维线弹性问题,其形式为
\[
\left(\phi_{j}\sum_{i=0}^{n}u_{i}\left.\frac{\partial \phi_{i}}{\partial x}\, \right)\right|^{x=L}_{x=0} + \sum_{i=0}^{n}u_{i}\int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x = \int_{0}^{L}f\,\phi_{j}\,\mathrm{d}x,\quad j=0:n.
\]
其中,\(\left\{\phi_{i}\right\}_{i=1}^{n}\) 是分片多项式函数空间的基函数,\(\left\{u_{i}\right\}_{i=1}^{n}\) 是待定求解的系数,通过求解线性方程组得到,于是有限元近似解为
\[
u_{h} = \sum_{i=1}^{n}u_{i}\phi_{i}.
\]
由于 \(\phi_{i}\) 是基于单元的分片多项式,因此不论是刚度矩阵的计算
\[
\int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x,
\]
还是场变量分布计算
\[
u_{h}(x,y) = \sum_{i=1}^{n}u_{i}\phi_{i}(x,y),
\]
都可以转换为单元上的计算
\[
\int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x = \sum_{E}\int_{E}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}E = \sum_{E}\int_{E}\frac{\partial \left.\phi_{i}\right|_{E}}{\partial x}\frac{\partial \left.\phi_{j}\right|_{E}}{\partial x}\,\mathrm{d}E
\]
和
\[
u_{h}(x,y) = \sum_{i=1}^{n}u_{i}\left.\phi_{i}(x,y)\right|_{E_{(x,y)}}
\]
因此,关键在于得到
\[
\begin{equation}
\left.\phi_{i}\right|_{E}
\end{equation}
\]
另一方面,由于 \(\phi_{i}\) 具有局部支性(即仅在与节点相邻的单元上取值非零),因此,对于 \(\phi_{i}\),只需关注那些使得 \(\phi_{i}\) 非零的单元(相邻单元)中的表达式,在这些单元中,\(\phi_{i}\) 具有以下性质
多项式:\(\left.\phi_{i}\right|_{E}\) 是多项式
插值性:在自身节点取值为 1, 其余节点取值为 0
连续性:在相邻单元边界处满足 \(C^{0}\) 连续
\(\left.\phi_{i}\right|_{E}\) 与单元 \(E\) 的几何形状密切相关,这给 \(\left.\phi_{i}\right|_{E}\) 的构造带来了高度的复杂性
为简化计算,通常基于参考单元(如二维标准三角形/矩形单元,三维标准四面体/六面体单元)构造基函数(形函数),再通过坐标变换将一般单元(物理单元)上的计算映射回参考单元
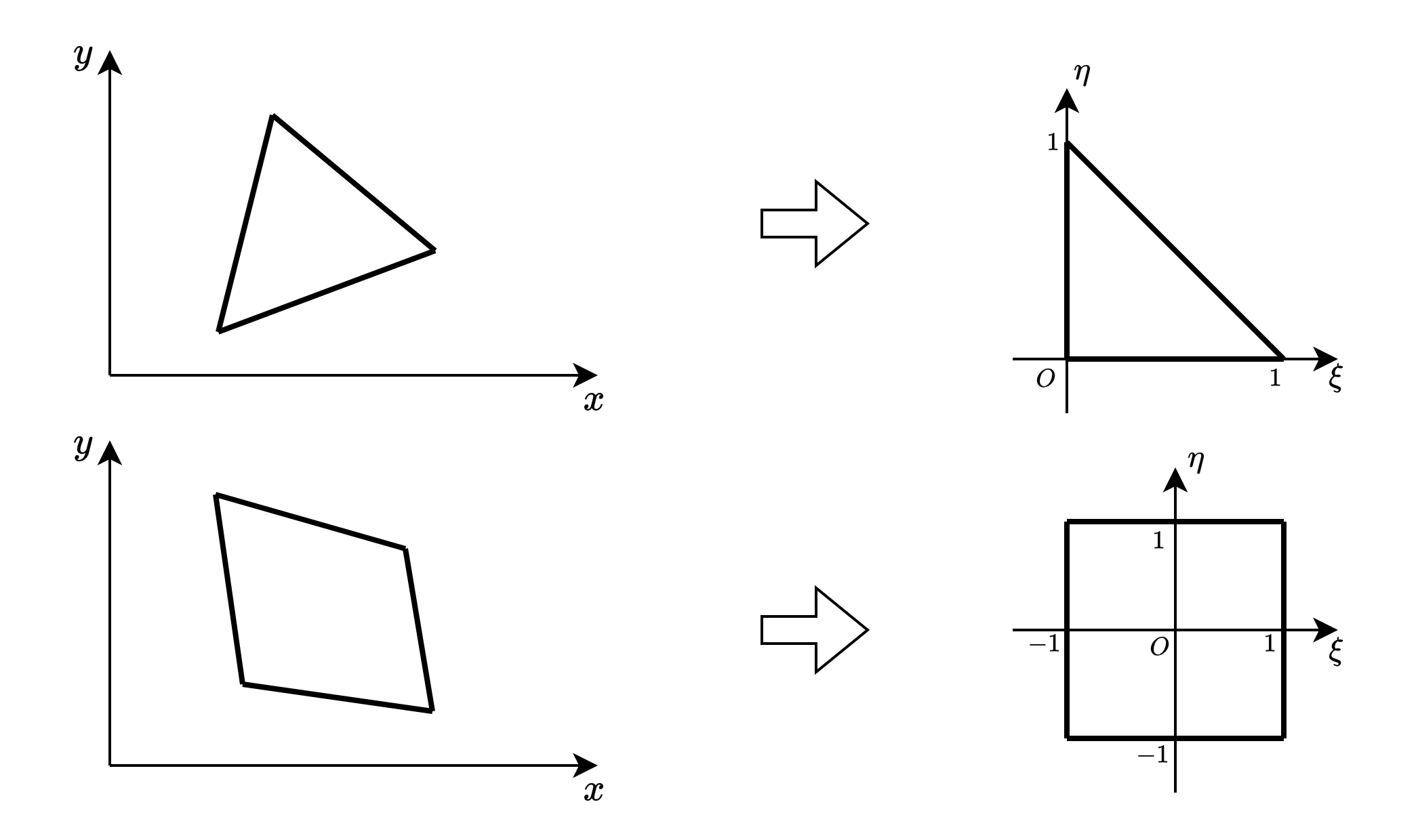
Fig. 5 从一般单元映射到参考单元#
这样,通过解耦基函数构造与单元几何形态,有效规避了复杂单元几何对基函数构造的影响,确保不同几何形态单元基函数表达的统一性
