数值方法简介

例如，在前面章节介绍的平面应力/应变问题中，物理量之间的关系便以偏微分方程的形式呈现

在科学与工程领域，许多实际问题都可以通过物理方程进行建模，例如结构受力分析、热传导、流体流动和电磁场分布等。这些物理方程通常以 偏微分方程 (PDE)的形式描述系统的基本规律，将复杂的自然现象抽象为数学模型。

然而，由于实际问题常伴随复杂的几何形状、边界条件、非线性效应以及材料的非均匀性，这些方程的解析解往往难以求得。 此时，数值求解方法成为连接理论模型与实际应用的关键工具，通过离散化和数值计算求解物理方程，为实际问题提供解决方案并支撑科学预测

有限差分法（FDM）、有限元法（FEM）和有限体积法（FVM）是求解偏微分方程的三大数值方法，各自具有独特的优势和适用场景：

1. 有限差分法：算法简单、计算效率高，适用于规则网格和简单几何问题，广泛应用于热传导、波动方程等简单物理问题

2. 有限元法：具有高度灵活性，能够处理复杂几何、非线性问题和异质材料，但实现较为复杂，计算量较大；广泛应用于固体力学、结构分析、电磁场等需要精细建模的领域

3. 有限体积法：严格满足局部守恒性，并具有良好的网格适应性，特别适合计算流体力学（CFD）和传热学等守恒律问题

接下来通过一个简单的例子，介绍三种数值方法的核心思想

问题描述

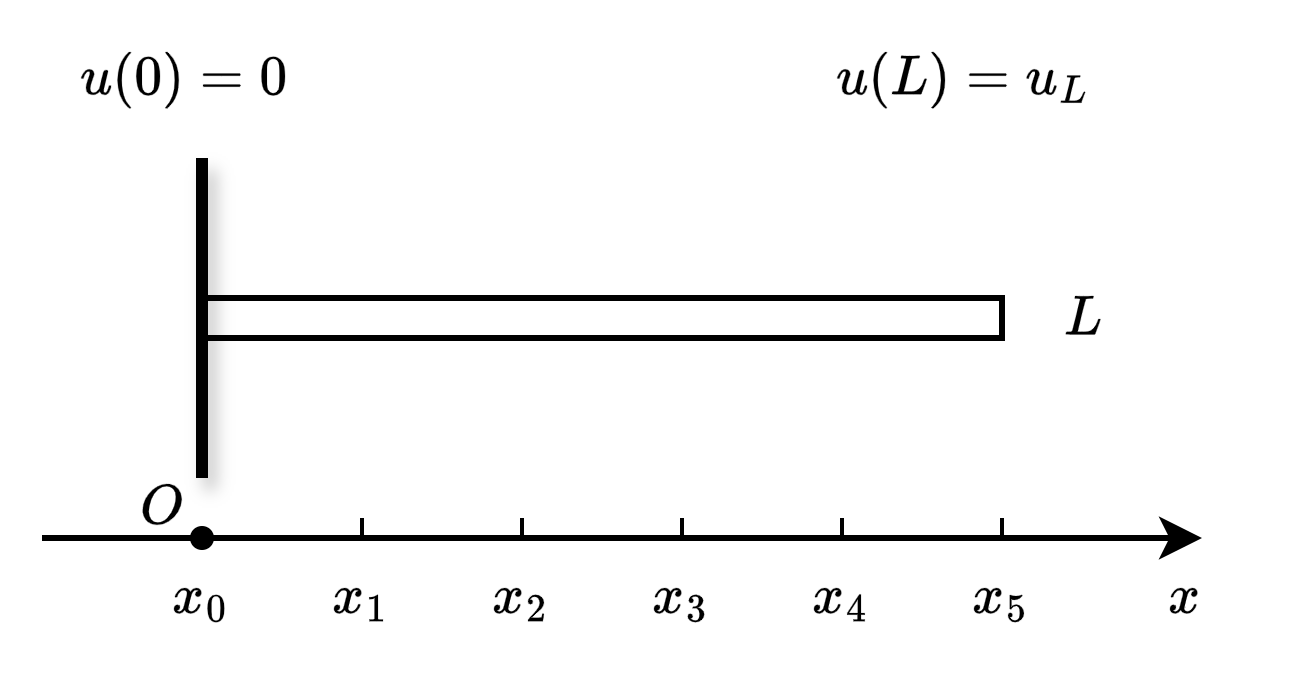
Fig. 33 一维均匀弹性杆

考虑一根长度为 \(L\) 的一维均匀弹性杆，受力后在长度方向上的位移 \(u(x)\) 满足以下控制方程：

该方程可通过平面应力问题，按位移求解方程 (41) 退化成一维问题得到；简便起见，令弹性模量 \(E=1\)

(46)\[ \frac{\partial^2 u}{\partial x^2} + f= 0,\quad 0\leq x \leq L \]

其中

体积力作为源项，外部力作为边界条件

1. \(f\) 为分布载荷（体积力），不考虑重力

2. 左端固定：\(u(0)=0\)，右端固定位移：\(u(L)=u_{L}\)

如果 \(f\) 恒等于常数 \(-C\)，则方程 (46) 是容易求得的，它具有形式

\[ u(x) = Cx^2 + c_{1}x + c_{0} \]

代入边界条件：\(u(0)=0\) 和 \(u(L)=u_{L}\)，得到

\[ c_{0} = 0,\quad c_{1} = \frac{u_{L}-cL^2}{L}. \]

如果 \(f\) 的形式较为复杂，此时则无法得到 \(u\) 的解析表达式，这时需要借助数值求解的手段：

1. 将计算区域划分为若干个网格单元，如图所示，长度为 \(L\) 的线段被均匀划分为五个单元，每个单元的长度为 \(h\)

2. 在单元内部或单元节点上离散化控制方程，结合边界条件来求解目标方程

有限差分法

有限差分方法的基本思路是利用差分公式对导数进行离散化近似，从而将偏微分方程转化为代数方程，例如一阶差分

记 \(u(x_{n}) = u_{n}\)，\(f(x_{n}) = f_{n}\)

(47)\[ \left.\frac{\partial u}{\partial x}\right|_{x_{2}} = \frac{u_3-u_1}{h} + o(h)\approx \frac{u_3-u_1}{h}. \]

对于二阶导数，通常采用中心差分近似，即

(48)\[ \begin{equation} \begin{aligned} \left.\frac{\partial^2 u}{\partial x^2}\right|_{x_{n}}&\approx \frac{u_{n+1} - 2\,u_{n} + u_{n-1}}{h^2} \end{aligned} \end{equation} \]

令方程 (46) 在除边界节点外的每一个网格节点 \(x_{n}\) 上满足，则得到关于 \(u_{n}\) 的代数方程组

(49)\[\begin{split} \frac{u_{n+1} - 2\,u_{n} + u_{n-1}}{h^2} + f_n = 0,\quad n=1,2,3,4\\ \end{split}\]

将边界条件

\[ u_0 = 0,\quad u_5 = u_L \]

代入到方程 (49) 中，于是共四个求解方程和四个求解变量，写成矩阵形式为

这是一个稀疏矩阵（非零元数量稀少），常使用迭代法进行求解

(50)\[\begin{split} \begin{equation} \frac{1}{h^2}\left[ \begin{matrix} -2 & 1 & & \\ 1 & -2 & 1 & \\ & 1 & -2 & 1 \\ & & 1 & -2 \end{matrix}\right] \left[ \begin{matrix} u_1 \\ u_2 \\ u_3 \\ u_4 \end{matrix}\right]= \left[ \begin{matrix} -f_1\\ -f_2 \\ -f_3 \\ -f_4 - \frac{u_L}{h^2} \end{matrix}\right]. \end{equation} \end{split}\]

通过求解代数方程组 (50)，可以得到 \(u\) 在点 \(x_{1},x_{2},x_{3},x_{4}\) 的近似值。\(u\)在其它位置的值通常可以通过已知网格节点的值插值得到

随着 \(h \to 0\)，方程 (48) 左端与右端的近似精度逐渐提高，线性方程组 (49) 的解将越来越接近方程 (46) 的真解

有限元法

有限元法的核心思想是将计算区域划分为若干单元，在每个单元上选取简单的插值函数来近似真解，并通过离散化和组装形成整体方程，从而求解原问题的近似解

弱形式

光滑性：函数的高阶导数存在且连续。例如，若 \(f\) 连续，则要求 \(u\) 的二阶导数连续

方程 (46) 被称为问题的强形式，因为它要求解函数 \(u\) 在定义域内严格满足给定的微分方程及其边界条件。这意味着 \(u\) 必须具备足够的光滑性，以确保微分运算和边界条件的精确成立

在实际问题中，材料的不连续性、载荷的突变或几何的奇异点通常会导致强解（经典解）不存在或无法满足光滑性要求。通过将微分方程转化为积分形式，并通过分部积分降低解函数的光滑性要求，能够在更广泛的函数空间（如有限元函数空间）中寻求近似解，从而更有效地逼近问题的真实解

首先，选择试验函数 \(v\in \mathcal{V}\)，\(\mathcal{V}\) 是某个选定的函数空间，于是方程 (46) 写为

(51)\[ \int_{0}^{L}\left(\frac{\partial^2 u}{\partial x^2} + f\right)\cdot v \, \mathrm{d}x = 0,\quad \forall v\in \mathcal{V}. \]

方程 (51) 可以理解为 \(\frac{\partial^2 u}{\partial x^2} + f\) 在某个函数空间 \(\mathcal{V}\) 的投影为 0。可以预见，函数空间 \(\mathcal{V}\) 越大，就越接近于全空间，方程 (51)的解也就越接近于真解

例如，如果 \(\mathcal{V}\) 选为全函数空间，则此时方程 (51) 与强形式 (46) 是等价的，因为此时可以选择

\[ v = \frac{\partial^2 u}{\partial x^2} + f, \]

将其代入到方程 (51) 中，由连续性要求得到 \(\frac{\partial^2 u}{\partial x^2} + f \equiv 0, x\in [0,L]\)。

接下来，需要选定解函数 \(u\) 的逼近空间 \(\mathcal{U}\)，如果

• \(\mathcal{U} = \mathcal{V}\)：称为协调有限元

• \(\mathcal{U} \neq \mathcal{V}\)：称为非协调有限元

此时方程变为，求 \(u\in \mathcal{U}\) 满足

(52)\[ \int_{0}^{L}\left(\frac{\partial^2 u}{\partial x^2} + f\right)\cdot v \, \mathrm{d}x = 0,\quad \forall v\in \mathcal{V}. \]

使用分部积分，得到弱形式

通过分部积分公式，降低了对解函数 \(u\) 的光滑性要求，自然引入边界条件，还降低了（高阶导数）对分片多项式次数的要求（通过导数分配机制，构建解与测试函数空间的协同关系）

(53)\[ \left.\left(\frac{\partial u}{\partial x}\, v\right)\right|^{x=L}_{x=0}-\int_{0}^{L}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,\mathrm{d}x + \int_{0}^{L}f\, v \, \mathrm{d}x = 0,\quad \forall v\in \mathcal{V}. \]

Note

在有限元方法中，试验函数空间 \(\mathcal{V}\) 和解空间 \(\mathcal{U}\) 的选择至关重要。它不仅需要具备良好的逼近能力，以确保解的精度，还应具有易于数值计算的特性，从而提高计算效率

基函数

下标 \(h\) 表示与网格相关

弱形式 (53) 仍然是一个连续问题。为了求解该问题，需要对其进行离散化。因此需要在 \(\mathcal{V}\) 和 \(\mathcal{U}\) 中选取有限维的函数子空间 \(\mathcal{V}_{h}，\mathcal{U}_{h}\)，这些空间通常由分片多项式空间构成

在有限元方法中，分片多项式指的是在每个单元上均由多项式表示的函数，通常要求在单元交界处满足一定的连续性条件

下图给出了一个线性分片多项式空间 \(\mathcal{P}^{1}_h\) 的示例，其中，\(g\in\mathcal{P}^{1}_h\) 在每个网格单元上均为一次多项式

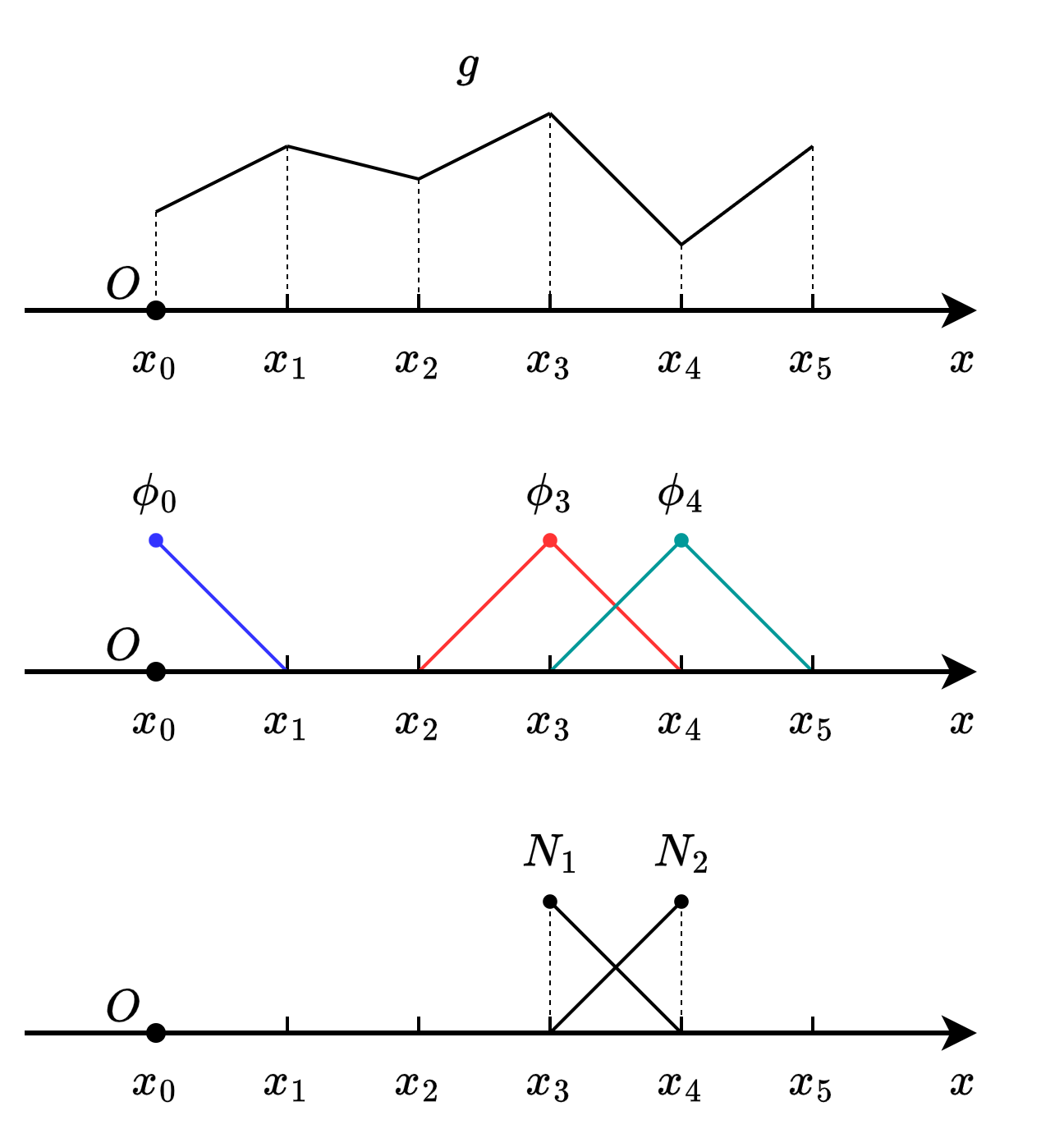
Fig. 34 分片多项式，基函数，形函数

\(\mathcal{P}^1_h=\text{span}\{\phi_{0},\phi_{1},...\}\)

\(g\) 可以表示为一组基函数的线性组合

\[ g = \sum_{i=0}^{5}c_{i}\phi_{i}, \]

其中，\(c_{i}\) 是系数。对于内部的节点（\(x_{1},x_{2},x_{3},x_{4}\)）

\(\phi_{i}\) 定义在网格节点上，因此被称为节点基，广泛用于拉格朗日元

\(\phi_{i}\) 仅在与其关联的单元上非零，而在其它单元上为零，这种局部支性使得刚度矩阵具有稀疏性

\[\begin{split} \phi_{i}= \begin{cases} \frac{x-x_{i-1}}{x_i-x_{i-1}},\quad &x\in[x_{i-1},x_{i}],\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},\quad &x\in[x_{i},x_{i+1}],\\ 0,\quad & \text{else}. \end{cases} \end{split}\]

对于边界的节点（例如 \(x_0\)），定义在其上的基函数为

\[\begin{split} \phi_{0}= \begin{cases} \frac{x-x_{1}}{x_0-x_{1}},\quad &x\in[x_{0},x_{1}],\\ 0,\quad & \text{else}. \end{cases} \end{split}\]

形函数在单元的节点处取值为 1，在其他节点处取值为 0

基函数在单元上的局部定义被称为形函数，例如 \(N_{1},N_{2}\)。形函数是基函数的局部化表达形式，用于描述单元内部的插值关系，是有限元方法中构造数值解的关键工具之一

刚度矩阵

此处，选取 \(\mathcal{U}_{h}=\mathcal{V}_{h}=\mathcal{P}^{1}_{h}\)，于是，得到弱形式 (53) 的离散形式：求解 \(u\in\mathcal{P}^{1}_{h}\) 满足

(54)\[ \left.\left(\frac{\partial u}{\partial x}\, v\right)\right|^{x=L}_{x=0}-\int_{0}^{L}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,\mathrm{d}x + \int_{0}^{L}f v \, \mathrm{d}x = 0,\quad \forall v\in \mathcal{P}^{1}_{h}. \]

算子 \(\mathcal{L}(x)\) 是线性的，即

\(\sum_{i=1}^{n}c_{i}\mathcal{L}(v_{i}) = \mathcal{L}(\sum_{i=1}^{n}c_{i}v_{i})\)

由于算子对 \(v\) 是线性的，上述问题等价于求解 \(u\in\mathcal{P}^{1}_{h}\) 满足

(55)\[ \left.\left(\frac{\partial u}{\partial x}\, \phi_{j}\right)\right|^{x=L}_{x=0}-\int_{0}^{L}\frac{\partial u}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x + \int_{0}^{L}f\phi_{j}\,\mathrm{d}x=0,\quad j=0:5. \]

由于 \(u\in\mathcal{P}^{1}_{h}\)，因此可以表示成

\[ u = \sum_{i=0}^{5}c_{i}\phi_{i}. \]

将上式代入到 (55)，得到

(56)\[ \left(\phi_{j}\sum_{i=0}^{5}c_{i}\left.\frac{\partial \phi_{i}}{\partial x}\, \right)\right|^{x=L}_{x=0} + \sum_{i=0}^{5}c_{i}\int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x = \int_{0}^{L}f\phi_{j}\,\mathrm{d}x,\quad j=0:5. \]

这是一个关于 \(c_{i}\) 的线性方程组

边界条件

对于内部节点 \(x_1,x_2,x_3,x_4\)，有

\[ \left(\phi_{j}\sum_{i=0}^{5}c_{i}\left.\frac{\partial \phi_{i}}{\partial x}\, \right)\right|^{x=L}_{x=0} = 0, \]

由于 \(u(0) = 0, u(L) = u_L\)，因此 \(c_{0} = 0, c_{5} = u_{L}\)，代入到式 (56) 中的 \(j=1,2,3,4\)，得到

(57)\[ \sum_{i=1}^{4}c_{i}\int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x = \int_{0}^{L}\left(f\phi_{j} - c_{5}\frac{\partial \phi_{5}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\right)\mathrm{d}x,\quad j=1:4. \]

将其写为矩阵形式

(58)\[\begin{split} \begin{equation} \frac{1}{h^2}\left[ \begin{matrix} -2 & 1 & & \\ 1 & -2 & 1 & \\ & 1 & -2 & 1 \\ & & 1 & -2 \end{matrix}\right] \left[ \begin{matrix} c_1 \\ c_2 \\ c_3 \\ c_4 \end{matrix}\right]= \left[ \begin{matrix} -f_1 \\ -f_2 \\ -f_3 \\ -f_4 - \frac{u_L}{h^2} \end{matrix}\right], \end{equation} \end{split}\]

左端矩阵被称为刚度矩阵，在右端项中

\[ f_{j} = \frac{1}{h}\int_{0}^{L}f\phi_{j}\,\mathrm{d}x. \]

通过求解线性方程组 (58)，可以得到 \(c_{i}\)，从而得到方程 (46) 在有限元函数空间 \(\mathcal{P}_{h}^1\) 的逼近解 \(u(x)\approx \sum_{i=0}^{5}c_{i}\phi_{i}\)

随着 \(h\to0\)，有限元函数空间 \(\mathcal{P}_{h}^1\) 中的函数能够以任意精度逼近任意连续函数，从而保证离散解逐渐逼近问题的真解

积分计算与形函数

刚度矩阵计算的关键在于计算积分式

\[ \int_{0}^{L}\frac{\partial \phi_{i}}{\partial x}\frac{\partial \phi_{j}}{\partial x}\,\mathrm{d}x \]

由于基函数的局部支性，当且仅当 \(i=j\) 或 \(i-j=\pm 1\) 时上式非 0。当

• \(i=j\) 时，积分式可以写为

\[ \int_{0}^{h}\left(\frac{\partial N_{1}}{\partial x}\frac{\partial N_{1}}{\partial x}+\frac{\partial N_{2}}{\partial x}\frac{\partial N_{2}}{\partial x}\right)\,\mathrm{d}x \]

• \(i-j=\pm1\) 时，积分式可以写为

\[ \int_{0}^{h}\frac{\partial N_{1}}{\partial x}\frac{\partial N_{2}}{\partial x}\,\mathrm{d}x \]

因此，基函数的积分计算最终可以转化为单元内部形函数的积分计算。当网格非均匀时，可以通过将目标单元映射到参考单元，利用几何变换将积分计算统一到参考单元中进行。这种方法不仅简化了积分的实现过程，还能适应复杂的网格划分，从而提高计算的灵活性和效率

有限体积法

有限体积法是一种通过对控制方程在离散控制体上积分，并利用守恒性将偏微分方程转化为离散代数方程的数值方法

为更清晰地展示该方法的核心思想，将弹性模量 \(E\) 体现在方程 (46) 中，令

注意到 \(\sigma\) 是应力

(59)\[ \sigma=E\,\frac{\partial u}{\partial x}, \]

于是方程 (46) 写为

(60)\[ \frac{\partial \sigma}{\partial x}+f=0,\quad 0\leq x \leq L. \]

这就是动量守恒方程在静力学条件下退化为静力平衡方程的情况，在每一个网格单元（控制体）中，对上式积分

(61)\[ \int_{x_{i}}^{x_{i+1}}\frac{\partial \sigma}{\partial x}\,\mathrm{d}x + \int_{x_{i}}^{x_{i+1}}f \,\mathrm{d}x=0,\quad i=0:4. \]

得到守恒方程的积分形式

守恒方程

守恒方程通常具备如下积分形式

(62)\[ \frac{\mathrm{d}}{\mathrm{d}t} \int_V m \, \mathrm{d}V + \int_{\partial V} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S - \int_V Q \, dV = 0. \]

其中，\(t\) 是时间，\(V\) 是控制体，\(\partial V\) 是 \(V\)的边界，\(\mathbf{n}\) 是 \(\partial V\) 的外法向；\(m\) 是守恒量的密度（如能量密度，质量密度），\(\mathbf{F}\) 是通量（如能量通量，质量通量），表示守恒量通过界面的速度，\(Q\) 是源汇项，表示控制体内守恒量生成或消耗的速率

因此，守恒方程描述的是：

控制体内守恒量的变化率 = 通过边界的净通量 + 内部生成或消耗量

对方程 (62) 使用散度定理，得到

(63)\[ \frac{\mathrm{d}}{\mathrm{d}t} \int_V m \, \mathrm{d}V + \int_{V} \nabla\cdot \mathbf{F} \, \mathrm{d}V - \int_V Q \, dV = 0. \]

由控制体的任意性，得到守恒方程的微分形式

(64)\[ \frac{\mathrm{d}\,m}{\mathrm{d}t}+ \nabla\cdot \mathbf{F} - Q = 0. \]

当系统处于稳态时，守恒量不再变化，因此

\[ \frac{\mathrm{d}}{\mathrm{d}t} \int_V m \, \mathrm{d}V = 0, \]

守恒方程 (62) 变为

\[ \int_{\partial V} \mathbf{F} \cdot \mathbf{n} \, \mathrm{d}S - \int_V Q \, dV = 0. \]

守恒方程 (64) 变为

\[ \nabla\cdot \mathbf{F} - Q = 0. \]

动量守恒方程

动量守恒方程的微分形式通常表示为

(65)\[ \frac{\partial (\rho \mathbf{v})}{\partial t} = - \nabla \cdot (\rho \mathbf{v} \otimes \mathbf{v}) + \nabla \cdot \boldsymbol{\sigma} + \mathbf{f}, \]

其中，\(t\) 是时间，\(\rho\) 是密度，\(\mathbf{v}\) 是速度向量，\(\boldsymbol{\sigma}\) 是应力张量，\(\mathbf{f}\) 是体积力，\(\otimes\) 是张量外积。该方程描述的是

动量变化率=对流通量（动量随物体运动的输运）+表面力引起的动量通量（应力张量的贡献）+体积力贡献

动量守恒方程可以退化为固体力学中的静力平衡方程，当固体处于静态条件下，速度 \(\mathbf{v}\) 为零，方程 (65) 变为

\[ \nabla \cdot \boldsymbol{\sigma} + \mathbf{f} = 0. \]

一维情况下退化为积分公式

对第一项应用散度定理，得到

(66)\[ \sigma_{i+1}-\sigma_{i} + \int_{x_{i}}^{x_{i+1}}f\,\mathrm{d}x = 0,\quad i=0:4. \]

\(\sigma_{i}\) 是单元界面处的应力，可使用两点通量格式对其近似

高维情况下还需考虑界面面积的加权

(67)\[ \sigma_{i} = \left.\left(E\,\frac{\partial u}{\partial x}\right)\right|_{x=x_{i}}=\frac{2E_{i-\frac{1}{2}}E_{i+\frac{1}{2}}}{E_{i-\frac{1}{2}}+E_{i+\frac{1}{2}}}\cdot \frac{u_{i+\frac{1}{2}}-u_{i-\frac{1}{2}}}{h},\quad i=0:4. \]

其中 \(u_{i+\frac{1}{2}}\) 表示网格单元 \([x_{i},x_{i+1}]\) 内的 \(u(x)\) 的平均水平

Note

注意到，两点通量格式 (67) 和有限差分格式 (47) 在形式上虽然接近，但本质上存在重要的差别

1. 理论基础的差异：有限差分方法是通过对导数进行数值近似来求解偏微分方程，其核心关注点是导数值的准确性；而通量格式（有限体积方法）是通过对通量进行近似来保证守恒性，重点在于物理量的局部守恒

2. 考虑信息的不同：有限差分方法在构造格式时通常只依赖几何信息，例如网格节点的分布和单元尺寸；而有限体积方法除了几何信息外，还需要考虑物理信息，例如材料的弹性模量 \(E \) 或其他物理参数，以确保通量的准确计算。

3. 变量意义的差异：有限差分方法中，\(u_{i}\) 是对函数值 \(u(x_{i})\) 的近似，反映的是离散节点上的函数值；而在有限体积方法中，\(u_{i+\frac{1}{2}}\) 是对网格单元 \([x_{i},x_{i+1}]\) 内物理量的平均值近似，反映的是单元内部的均质性假设。

基于上述差别，有限差分方法适用于网格规则且物理特性简单的场景，而有限体积方法由于其对守恒性的严格保证和对物理信息的考虑，能够更自然地适应复杂网格和具有复杂物理特性的场景

边界条件

可以在网格的左右两端分别引入一个虚拟单元，单元尺寸为 \(h\)，端点位置分别为 \(x_{-1}\) 和 \(x_{6}\)。根据边界条件，可得 \(u_{-\frac{1}{2}} = 0\)，\(u_{5+\frac{1}{2}} = u_{L}\)

为简化问题，将 \(E\equiv1\) 代回到方程 (67) 中。根据方程 (67) 和边界条件，建立关于 \(u_{i+\frac{1}{2}}\) 的线性方程组

(68)\[\begin{split} \begin{equation} \frac{1}{h^2}\left[ \begin{matrix} -2 & 1 & & & \\ 1 & -2 & 1 & & \\ & 1 & -2 & 1 & \\ & & 1 & -2 & 1 \\ & & & 1 & -2 \end{matrix}\right] \left[ \begin{matrix} u_{0+\frac{1}{2}} \\ u_{1+\frac{1}{2}} \\ u_{2+\frac{1}{2}} \\ u_{3+\frac{1}{2}} \\ u_{4+\frac{1}{2}} \end{matrix}\right]= \left[ \begin{matrix} -f_{0+\frac{1}{2}} \\ -f_{1+\frac{1}{2}} \\ -f_{2+\frac{1}{2}} \\ -f_{3+\frac{1}{2}} \\ -f_{4+\frac{1}{2}} - \frac{u_L}{h^2} \end{matrix}\right], \end{equation} \end{split}\]

其中

\[ f_{i+\frac{1}{2}} = \frac{1}{h}\int_{x_{i}}^{x_{i+1}}f\,\mathrm{d}x. \]

通过求解线性方程组 (68)，可以求解 \(u(x)\) 在每个网格单元内的近似解

随着 \(h\to0\)，每个网格单元的尺寸逐渐减小，此时 \(u_{i+\frac{1}{2}}\) 越能准确代表单元 \([x_{i},x_{i+1}]\) 内部的平均水平。此外，通量公式的计算精度也随之提高，因此方程 (68) 的解将逐渐逼近问题的真实解

See also

注意到，式 (50)，式 (58) 与式 (68) 得到了相同形式的离散矩阵。这表明，这三种数值方法在解决简单问题时具有一定的共性

数值仿真

“数值仿真是现代科学与工程领域中不可或缺的重要工具，其核心在于通过数值算法求解偏微分方程，以模拟和分析复杂物理现象。偏微分方程是许多自然规律的数学描述，例如描述流体运动的纳维-斯托克斯方程、描述固体变形的弹性力学方程，以及描述热传导的热传导方程等。而数值算法通过将这些连续的数学模型离散化，使其能够在计算机上进行求解，从而帮助人们理解和预测复杂系统的行为

在流体力学领域，数值仿真可以用来研究空气动力学中的飞行器设计、水动力学中的船舶性能优化，以及气候模拟中的大气与海洋相互作用。例如，通过求解纳维-斯托克斯方程，工程师可以优化飞机机翼的形状，以降低阻力并提高燃油效率；在水利工程中，数值仿真可以帮助设计防洪设施，预测洪水的传播路径和影响范围

在固体力学领域，数值仿真广泛应用于结构分析、材料设计和地质工程等方面。例如，通过求解弹性力学方程，可以分析建筑结构在地震或风载荷下的变形与应力分布，从而提高建筑的安全性；在材料科学中，数值仿真可以帮助研究新型材料的力学性能，例如预测复合材料在复杂载荷下的行为；在地质工程中，数值仿真可以用于评估隧道开挖对周围岩体的稳定性影响

数值仿真的重要性还体现在其成本效益上。在许多情况下，通过实验直接研究复杂系统的行为可能代价高昂甚至不可行，而数值仿真则提供了一种高效且可控的替代方案。例如，在航空航天领域，数值仿真可以大幅减少风洞实验的次数；在核工业中，数值仿真能够模拟核反应堆的运行状态，确保系统的安全性

总之，数值仿真通过将偏微分方程与数值算法相结合，为研究和解决复杂的科学与工程问题提供了强有力的工具。它不仅推动了流体力学、固体力学等领域的发展，还在能源、环境、医疗等跨学科领域中发挥着越来越重要的作用”

—— GPT-4o 😀