\[
\int_{E_\text{物理}}f(x,y)\,\mathrm{d}x\mathrm{d}y=\int_{E_\text{参考}}f(\xi,\eta)\cdot\left|\det \mathbf{J}\,\right|\ \mathrm{d}\xi\mathrm{d}\eta,
\]
\[\begin{split}
\begin{equation}
\mathbf{J} = \left[
\begin{matrix}
\frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} \\
\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta}
\end{matrix}
\right].
\end{equation}
\end{split}\]
积分变换公式
在二维情形下，考虑坐标变换 \(T\)
\[
T:(\xi,\eta) \rightarrow (x(\xi,\eta),y(\xi,\eta))
\]
该变换将区域 \(\mathcal{D}\) 映射为区域 \(\mathcal{D}'\)。
如图所示，设点 \(P\) 被映射到了 \(P'\)
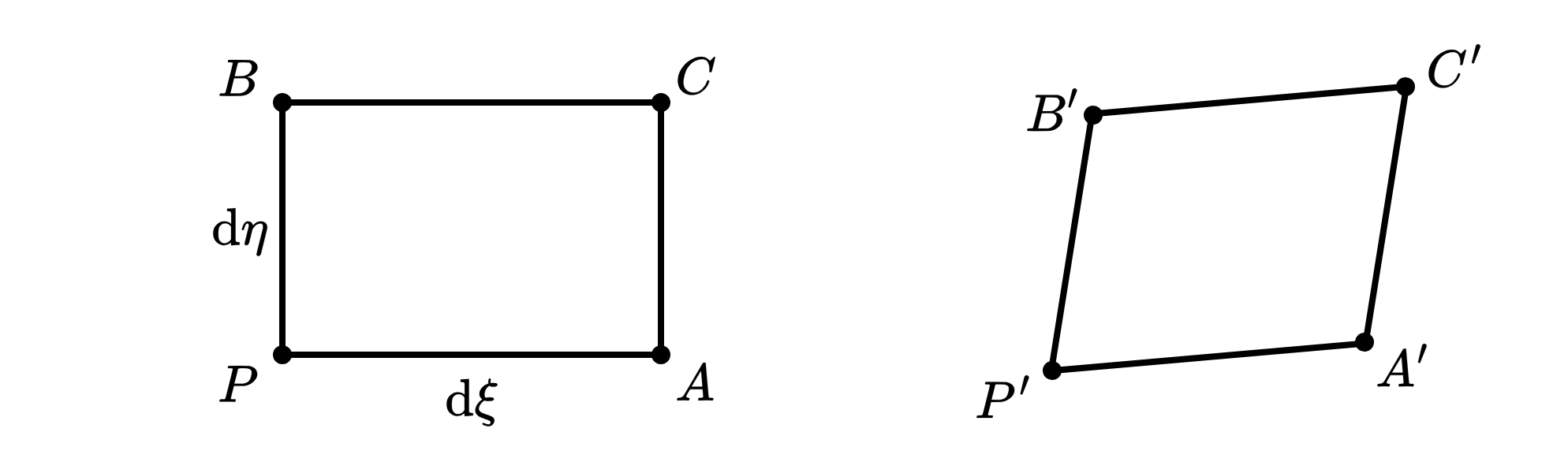
Fig. 17 二维情形下面积变换公式
于是，忽略高阶项，\(A',B',C'\) 的坐标位置为
\[\begin{split}
\begin{equation}
\begin{aligned}
x_{A'}&=x(\xi+\mathrm{d}\xi,\eta)\approx x +\frac{\partial x}{\partial \xi}\mathrm{d}\xi,\\
y_{A'}&=y(\xi+\mathrm{d}\xi,\eta)\approx y +\frac{\partial y}{\partial \xi}\mathrm{d}\xi,\\
x_{B'}&=x(\xi,\eta+\mathrm{d}\eta)\approx x +\frac{\partial x}{\partial \eta}\mathrm{d}\eta,\\
y_{B'}&=y(\xi,\eta+\mathrm{d}\eta)\approx y +\frac{\partial y}{\partial \eta}\mathrm{d}\eta,\\
x_{C'}&=x(\xi+\mathrm{d}\xi,\eta+\mathrm{d}\eta)\approx x +\frac{\partial x}{\partial \xi}\mathrm{d}\xi + \frac{\partial x}{\partial \eta}\mathrm{d}\eta,\\
y_{C'}&=y(\xi+\mathrm{d}\xi,\eta+\mathrm{d}\eta)\approx y +\frac{\partial y}{\partial \xi}\mathrm{d}\xi + \frac{\partial y}{\partial \eta}\mathrm{d}\eta.
\end{aligned}
\end{equation}
\end{split}\]
因此四边形 \(P'A'C'B'\) 是平行四边形，其面积为
\[
\begin{equation}
S_{P'A'C'B'} = \left|\overrightarrow{P'A'}\times\overrightarrow{P'B'}\right| = \left|\det(\mathbf{J})\right|\,\mathrm{d}\xi\mathrm{d}\eta,
\end{equation}
\]
因此
\[
\frac{S_{P'A'C'B'}}{S_{PACB}} = \left|\det(\mathbf{J})\right|.
\]
于是
\[\begin{split}
\begin{equation}
\begin{aligned}
\mathcal{D'} &= \int_{\mathcal{D'}}\mathrm{d}x\mathrm{d}y =
\lim_{n\rightarrow\infty}\sum_{n}\mathrm{d}\mathcal{D'}\\
&=\lim_{n\rightarrow\infty}\sum_{n}\left|\det(\mathbf{J})\right|\mathrm{d}\mathcal{D} = \int_{\mathcal{D}}\left|\det(\mathbf{J})\right|\ \mathrm{d}\xi\mathrm{d}\eta.
\end{aligned}
\end{equation}
\end{split}\]
类似地
\[
\int_{\mathcal{D'}}f(x,y)\ \mathrm{d}x\mathrm{d}y = \int_{\mathcal{D'}}f(\xi,\eta)\cdot\left|\det(\mathbf{J})\right|\ \mathrm{d}\xi\mathrm{d}\eta.
\]
对于 \(n\) 维的情形
\[
\int_{\mathcal{D'}}f(x,y,\cdots)\ \mathrm{d}\mathcal{D'} = \int_{\mathcal{D'}}f(\xi,\eta,\cdots)\cdot\left|\det(\mathbf{J})\right|\ \mathrm{d}\mathcal{D}
\]
其中
\[\begin{split}
\mathbf{J} = \left[
\begin{matrix}
\frac{\partial x}{\partial \xi} & \frac{\partial y}{\partial \xi} & \cdots \\
\frac{\partial x}{\partial \eta} & \frac{\partial y}{\partial \eta} & \cdots \\
\vdots & \vdots & \ddots
\end{matrix}
\right].
\end{split}\]
