单轴拉伸实验

单轴拉伸实验#

实验现象#

以金属棒的单轴拉伸实验为例，实验分为三个阶段：

  • 阶段1：初始弹性加载（\(O_{0} \rightarrow Y_{0}\)）

  • 阶段2：首次塑性加载与卸载（\(Y_{0} \rightarrow Z_{0} \rightarrow O_{1}\)）

  • 阶段3：再加载与新塑性阶段（\(O_{1} \rightarrow Y_{1} \rightarrow Z_{1}\)）

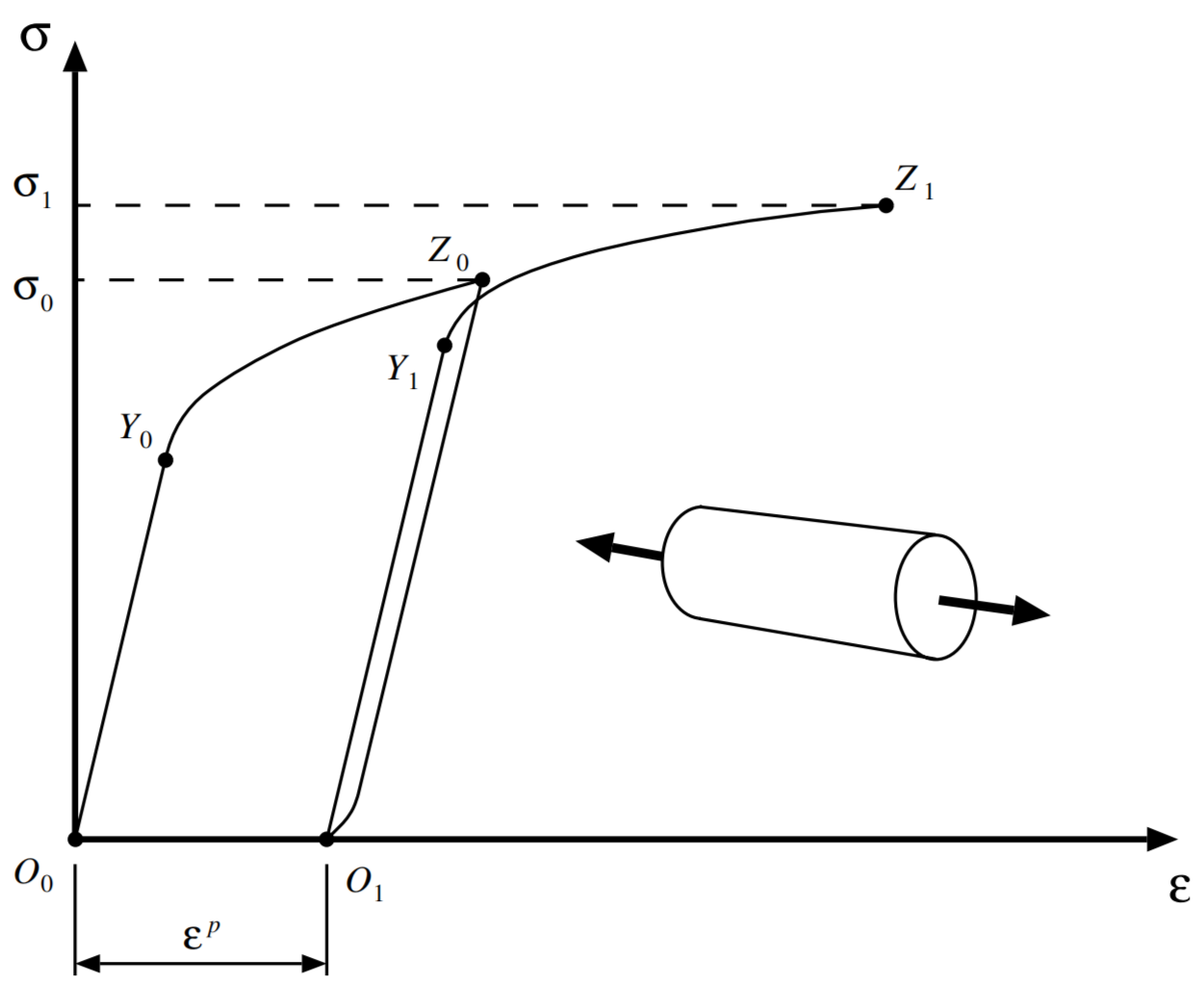
../../../_images/uniaxial.png

Fig. 37 金属单轴拉伸应力-应变曲线#

  • 阶段1：在 \(Y_{0}\) 之前，应力与应变成线性比例（胡克定律），斜率为弹性模量 \(E\)，若在 \(Y_{0}\) 点前卸载，则材料沿原路径返回 \(O_{0}\)，无残余应变

  • 阶段2：超过 \(Y_{0}\) （屈服极限）后，材料进入塑性阶段（斜率显著变化），此时，应变包含弹性部分和塑性部分；从 \(Z_{0}\) 开始卸载，应力-应变沿近似平行于初始弹性段的直线下降至 \(O_{1}\)，此时应力和弹性应变降至 0，存在永久塑性应变 \(\varepsilon_{p}\)

  • 阶段3：再加载，\(O_{1} \rightarrow Y_{1}\) 仍为弹性段，但屈服极限提高至 \(\sigma_{Y_{1}}\)，超过 \(Y_{1}\) 后，开始发生塑性流动

材料案例

  • 金属（典型延性材料）：适用于单轴拉伸或压缩试验，能够直接观察到材料的弹性区域、塑性流动以及硬化行为，其中硬化主要表现为各向同性

  • 土壤/岩石（非延性材料）：几乎不存在抗拉强度，单轴拉伸试验意义不大。通常通过三轴剪切试验来研究其剪切塑性变形特性

  • 混凝土、复合材料：表现出拉压不对称的力学行为，损伤与塑性变形相互耦合。需结合多轴加载和非比例路径试验捕捉材料的各向异性特征

本构模型#

理想应力-应变曲线#

对应力-应变曲线进行简化，得到理想应力-应变曲线。在理想化曲线中

  • 弹性区域与弹塑性区域之间的过渡体现为曲线斜率的非连续变化

  • 假设塑性应变不影响弹性应变，因此卸载和重新加载曲线之间的差异被忽略，卸载起始点 \(Z_{0}\) 与随后重新加载时的塑性屈服起始点 \(Y_{1}\) 重合，且初始加载/卸载/重新加载弹性段斜率一致

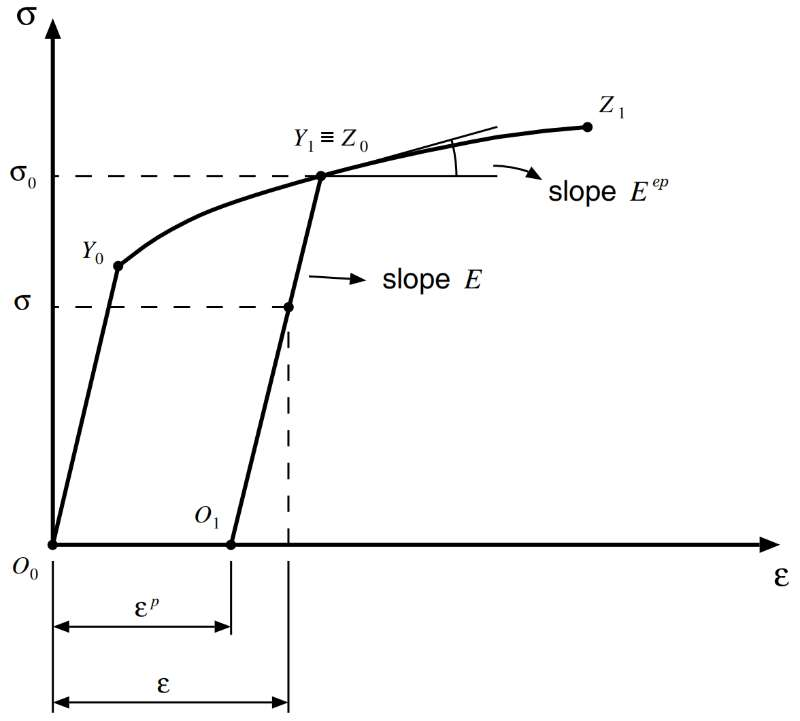
../../../_images/uniaxial-model.png

Fig. 38 理想应力-应变曲线#

应变的加法分解#

塑性力学小应变理论的基本假设是将总应变分解为弹性应变（可逆）和塑性应变（不可逆）：

\[ \varepsilon = \varepsilon^{e} + \varepsilon^{p}, \]

其中

  • 弹性应变：\(\sigma = E\varepsilon^{e} = E(\varepsilon-\varepsilon^{p})\)

  • 塑性应变：\(\varepsilon^{p}\) 为永久变形，与加载历史有关

屈服函数#

定义屈服函数用于判断材料是否进入塑性流动

\[ \Phi(\sigma,\sigma_{y}) = \left|\sigma\right| - \sigma_{y}, \]

其中，\(\sigma_{y}\) 为当前屈服应力。定义弹性域为

\[ \mathcal{E} = \{ \sigma \mid \Phi(\sigma, \sigma_y) < 0 \} \quad \text{即} \quad |\sigma| < \sigma_y, \]

当

  • \(\Phi<0\)：材料处于弹性状态（\(\dot{\varepsilon}=0\)）

  • \(\Phi=0\)：材料处于屈服边界，可能发生弹性卸载（\(\dot{\varepsilon}^{p}=0\)）或塑性加载（\(\dot{\varepsilon}^{p}\neq0\)）

在塑性加载过程中，‌应力状态的演化必须与屈服面的变化同步

\[ \Phi\equiv0 \quad \rightarrow \quad \dot{\Phi}\equiv0, \]

被称为一致性条件

塑性流动规则#

塑性应变速率 \(\dot{\varepsilon}^{p}\) 可正（拉伸），可负（压缩），定义塑性乘子，表示塑性流动的速率

\[ \dot{\varepsilon}^{p} = \dot{\gamma}\cdot\text{sign}(\sigma), \]

因此

\[ \dot{\gamma}\geq0. \]

塑性流动的发生（从弹性状态转为塑性状态）需满足互补条件

\[ \begin{align} \Phi\cdot\dot{\gamma} &= 0, \end{align} \]

互补条件用来控制塑性流动的启停，明确区分弹性与塑性阶段

硬化法则#

硬化法则用于描述材料在塑性变形过程中‌屈服应力随塑性应变增加而演化‌的现象（即材料变硬或变软），硬化函数

\[ \sigma_{y} = \sigma_{y}(\bar{\varepsilon}^{p}), \]

其中，\(\bar{\varepsilon}^{p}\) 是累积轴向塑性应变

\[ \bar{\varepsilon}^p \equiv \int_0^t |\dot{\varepsilon}^p| \, \mathrm{d}t, \]

因此，在单调拉伸试验‌中，有

\[ \bar{\varepsilon}^p = \varepsilon^p, \]

在单调压缩试验‌中，有

\[ \bar{\varepsilon}^p = -\varepsilon^p, \]

因此

\[ \dot{\bar{\varepsilon}}^p = \left|\dot{\varepsilon}^{p}\right|=\dot{\gamma}. \]

硬化函数 \(\sigma_{y}(\bar{\varepsilon}^{p})\) 的图像被称称为硬化曲线

塑性乘子#

在塑性加载过程中，满足

\[ \dot{\Phi} = \text{sign}(\sigma) \cdot \dot{\sigma} - H \cdot \dot{\bar{\varepsilon}}^p = 0, \]

其中 \(H=\frac{\partial \sigma_{y}}{\partial \bar{\varepsilon}^p}\) 为硬化模量，反映材料进入塑性变形阶段后‌进一步发生塑性变形的难易程度‌，当

  • \(H>0\)：材料表现出硬化特性，即在屈服后其承载能力增强，更难变形

  • \(H=0\)：材料表现为理想塑性，即屈服后承载能力保持不变

  • \(H<0\)：材料表现出软化特性，即在屈服后其承载能力下降，更易变形

将

(69)#\[ \begin{equation} \dot{\sigma} = E(\dot{\varepsilon} - \dot{\varepsilon}^p) = E(\dot{\varepsilon} - \dot{\gamma} \cdot \text{sign}(\sigma)), \end{equation} \]

和

\[ \dot{\bar{\varepsilon}}^p =\dot{\gamma}, \]

代入上式得到

\[ E(\dot{\varepsilon} \cdot \text{sign}(\sigma) - \dot{\gamma}) - H\dot{\gamma} = 0, \]

因此

(70)#\[ \begin{equation} \dot{\gamma} = \frac{E}{H + E} \cdot \text{sign}(\sigma) \cdot \dot{\varepsilon} = \frac{E}{H + E} |\dot{\varepsilon}|. \end{equation} \]

弹塑性切线模量#

将式 (70) 代入到应力率表达式 (69)中，得到

(71)#\[ \begin{equation} \dot{\sigma} = E \dot{\varepsilon} \left(1 - \frac{E}{E + H}\right) = \frac{EH}{E + H} \dot{\varepsilon}, \end{equation} \]

记

\[ E_{ep} := \frac{EH}{E+H}, \]

由于

\[ \begin{equation} E_{ep}=\frac{\dot{\sigma}}{\dot{\varepsilon}} = \frac{\partial \sigma}{\partial \varepsilon}, \end{equation} \]

因此，\(E_{ep}\) 是应力-应变曲线的切线斜率，被称为弹塑性切线模量，反映了材料在塑性阶段的刚度，用于表征材料在已发生塑性变形‌时对变形的瞬时抵抗能力。注意到

\[ E_{ep} < E, \]

且随硬化模量 \(H\) 增大而增大

此外，可以用 \(E_{ep}\) 表示硬化模量 \(H\)

\[ H = \frac{E^{ep}}{1 - E^{ep}/E}. \]

更多现象#

下图展示了退火延性多晶金属试样的典型单轴拉伸/压缩试验的应力-应变曲线，假设在实验条件下，温度低于材料熔点的一半，应变不超过 (10%)，应变速率在 \(10^{-2} - 10 \, \text{s}^{-1}\) 的范围内

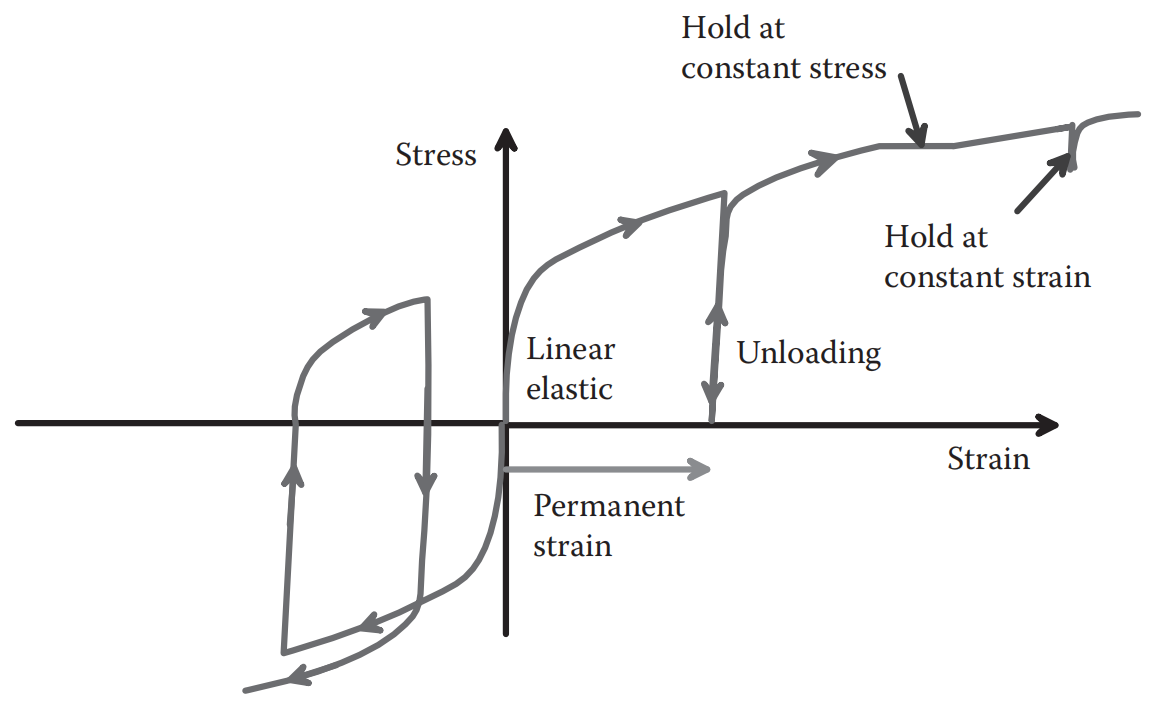
../../../_images/plasticity.png

Fig. 39 退火延性多晶金属试样的典型拉伸/压缩应力-应变曲线#

应力松弛#

应力松弛是指材料在恒定应变（或形变）条件下，内部应力随时间逐渐衰减的现象。其本质是材料内部结构的重新排列和粘弹性效应，导致应力重新分布。例如：

  • 在高温环境中，螺栓长期处于紧固状态时，部分弹性变形会转化为塑性变形，导致锁紧力逐渐降低

  • 橡胶密封圈在长期压缩后，其弹性性能可能下降，导致密封效果减弱

蠕变#

蠕变是指材料在恒定应力作用下，应变随时间逐渐增加的现象，尤其在高温条件下更为显著。蠕变通常分为三个阶段：

  • 初始蠕变阶段（瞬态蠕变）：在这一阶段，材料的应变速率逐渐减小，主要是由于材料内部结构开始调整

  • 稳态蠕变阶段（恒速蠕变）：此时，材料的应变速率保持恒定，是蠕变过程的主要部分。稳态蠕变阶段的持续时间最长，材料在此阶段表现出稳定的变形行为

  • 加速蠕变阶段（终态蠕变）：在这一阶段，应变速率迅速增加，直至材料失效。此阶段通常伴随着显著的微观结构变化，如孔洞形成和裂纹扩展，最终导致材料断裂

Bauschinger 效应#

Bauschinger 效应是指材料在经历一个方向的塑性变形后，当载荷反向施加时，其屈服强度降低的现象。具体来说，如果材料先在一个方向上受到力并发生塑性变形（如压缩），然后在相反方向上施加力（如拉伸），材料开始屈服的强度（拉伸）会比初始方向施加力时的屈服强度（压缩）低。这种效应是由于材料内部的位错结构在反向加载时重新排列，使得材料更容易发生变形

注记#

屈服应力#

材料的屈服应力通常难以精确确定，因为塑性变形涉及从微观结构变化到宏观行为的渐进过程

周期性加载#

在周期性加载下，材料的响应往往非常复杂，可能表现出周期性的硬化或软化

不可压缩性#

在塑性变形过程中，金属材料的密度保持恒定，这意味着材料在外力作用下会发生形状改变（如拉长、压扁），但不会发生体积变化。这是由于金属中的原子排列紧密且规则，塑性变形主要通过剪切应力引发的晶格中位错滑移和重排实现，而非通过体积压缩。因此，金属在塑性变形过程中表现出体积不变性

塑性本构模型的分类#

塑性本构模型通常分为两类：

  • 速率无关塑性：材料的塑性变形仅由当前应力状态和变形历史决定，与加载速率（应变率）或时间无关

    • 典型应用场景：金属在常温下的准静态加载，如冷轧和冲压

  • 速率相关塑性：材料的塑性变形不仅与当前应力状态和变形历史相关，还显著依赖于加载速率（应变率）或时间

    • 典型应用场景：高温下的金属蠕变、聚合物变形以及高速冲击问题

在这两大类模型中，存在许多不同的具体模型。这些模型主要在屈服准则，流动法则，硬化规律三个方面存在不同。目前，没有一个完全通用的模型能够涵盖所有特征，因此在具体应用中，需要识别材料行为中最关键的方面，并选择一个能够准确表征该行为的模型

Contents