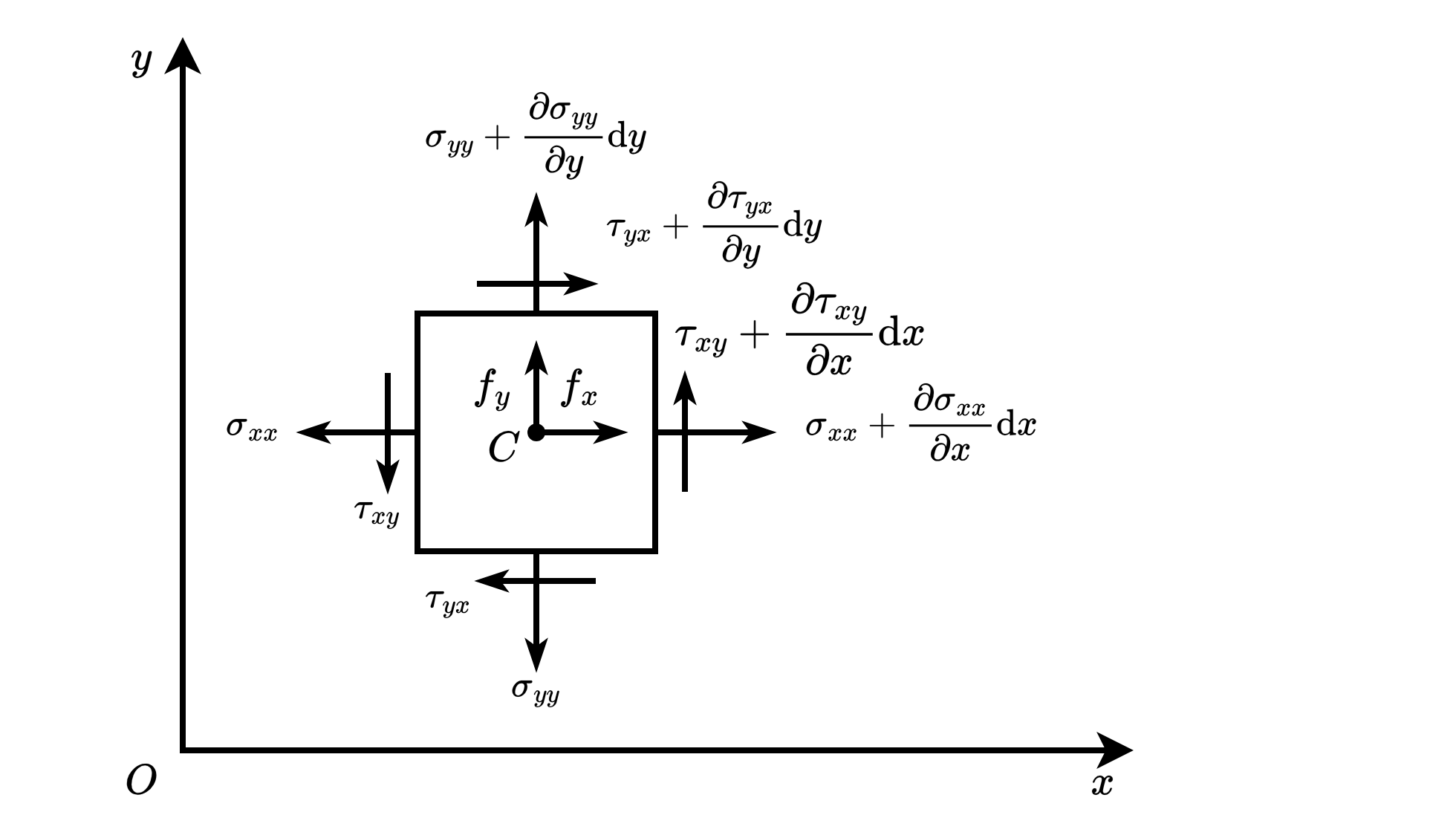
切应力互等定理
考虑以 \(C\) 点为中心的力矩平衡方程 \(\Sigma M_{C}=0\):
\[ \begin{align}\begin{aligned}\begin{split}
\tau_{xy}\cdot\mathrm{d}y\cdot\frac{1}{2}\mathrm{d}x+\left(\tau_{xy}+\frac{\partial \tau_{xy}}{\partial x}\mathrm{d}x\right)\cdot\mathrm{d}y\cdot\frac{1}{2}\mathrm{d}x-\\\end{split}\\\tau_{yx}\cdot\mathrm{d}x\cdot\frac{1}{2}\mathrm{d}y-\left(\tau_{yx}+\frac{\partial \tau_{yx}}{\partial y}\mathrm{d}y\right)\cdot\mathrm{d}y\cdot\frac{1}{2}\mathrm{d}x=0,
\end{aligned}\end{align} \]
整理得到
\[
\tau_{xy}+\frac{1}{2}\frac{\partial \tau_{xy}}{\partial x}\mathrm{d}x=\tau_{yx}+\frac{1}{2}\frac{\partial \tau_{yx}}{\partial y}\mathrm{d}y,
\]
于是得到切应力互等方程
(43)\[
\tau_{xy}=\tau_{yx}.
\]
平衡方程
考虑 \(x\) 轴方向的平衡方程 \(\Sigma F_{x}=0\):
\[
\left( \sigma_{xx} + \frac{\partial \sigma_{xx}}{\partial x} dx \right) \cdot dy
-\sigma_{xx} \cdot dy
+
\left( \tau_{yx} + \frac{\partial \tau_{yx}}{\partial y} dy \right) \cdot dx
-\tau_{yx} \cdot dx
+f_x dx dy = 0,
\]
整理得到
\[
\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + f_x = 0.
\]
类似地,可得到 \(y\) 方向上的平衡方程。于是,二维问题中的平衡方程为
(44)\[\begin{split}
\begin{cases}
\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \tau_{yx}}{\partial y} + f_x = 0, \\
\frac{\partial \sigma_{yy}}{\partial y} + \frac{\partial \tau_{xy}}{\partial x} + f_y = 0.
\end{cases}
\end{split}\]
可以写为
\[
\nabla\cdot \boldsymbol{\sigma} + \mathbf{f} = \mathbf{0},
\]
其中,\(\boldsymbol{\sigma}\) 是应力张量(见后文),\(\mathbf{f}\) 是体积力向量
任一点的应力状态
在实际问题中,为了全面了解材料在外力作用下的受力状态,通常需要研究某一点在不同取向截面上的应力分布。定义在同一点不同取向截面上的应力之间是否存在内在联系?
对于任意点 \(P\) ,以它为中心取一个微元直角三角形 \(\triangle ABC\),其中 \(\overline{CA}\) 平行于 \(x\) 轴,长度为 \(\mathrm{d}x\),\(\overline{CB}\) 平行于 \(y\) 轴,长度为 \(\mathrm{d}y\),
设 \(\overline{AB}\) 的单位法向量为 \(\mathbf{n}=(l,m)\),长度为 \(\mathrm{d}s\),于是
\[
\mathrm{d}x = m\mathrm{d}s,\quad \mathrm{d}y = l\mathrm{d}s.
\]
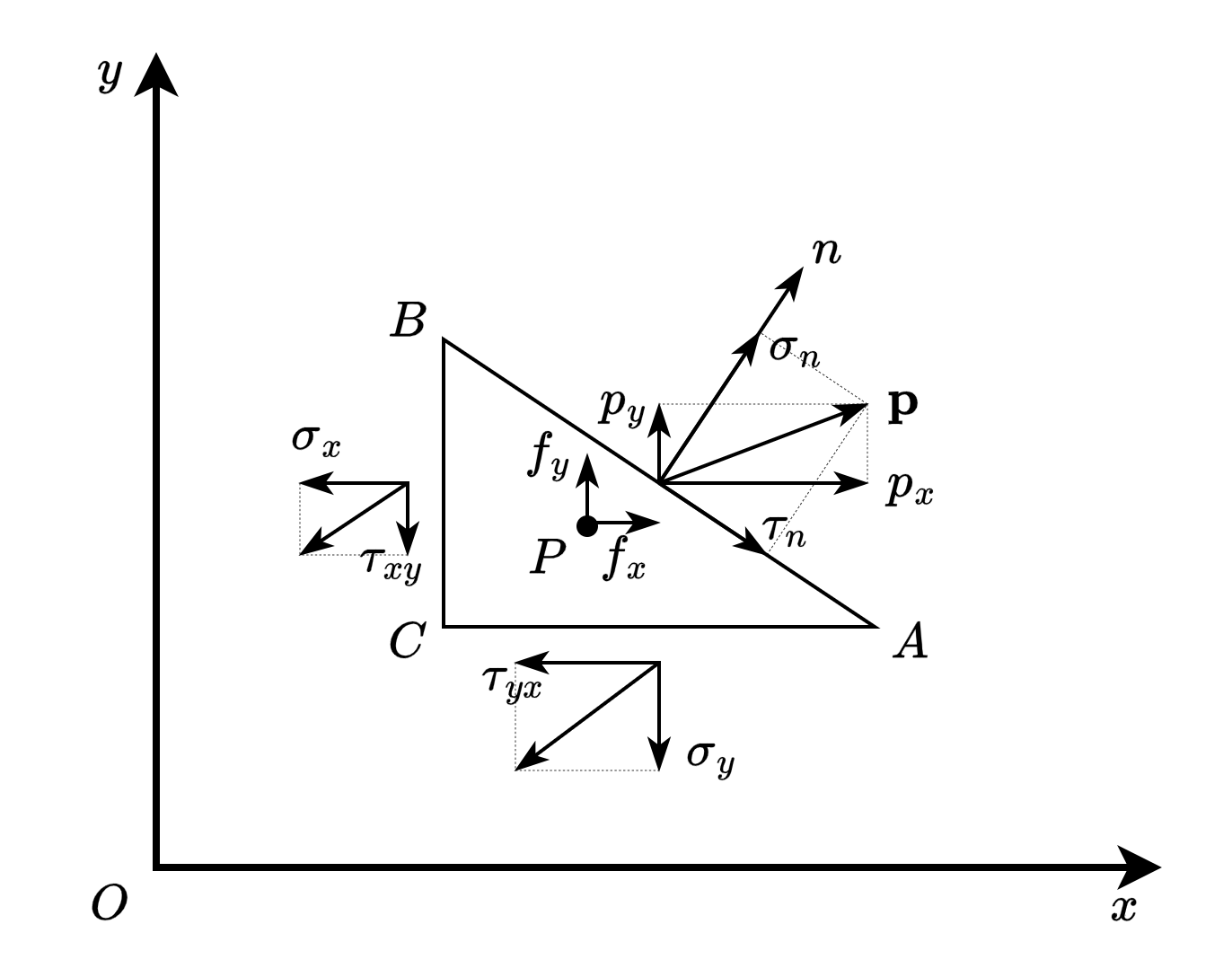
Fig. 28 任一点的应力状态
设 \(\overline{AB}\) 上全应力为 \(\mathbf{p}\),沿 \(x\) 轴方向和 \(y\) 方向的应力分量分别为 \(p_{x}\) 和 \(p_{y}\),分别建立沿 \(x\) 轴方向和 \(y\) 方向的平衡方程
\[\begin{split}
\begin{cases}
p_x \, \mathrm{d}s - \sigma_{xx} \, l\mathrm{d}s - \tau_{yx} \, m \mathrm{d}s + f_x \frac{l\mathrm{d}s \, m\mathrm{d}s}{2} = 0, \\
p_y \, \mathrm{d}s - \sigma_{yy} \, m \mathrm{d}s - \tau_{xy} \, l \mathrm{d}s + f_y \frac{l\mathrm{d}s \, m\mathrm{d}s}{2} = 0.
\end{cases}
\end{split}\]
消去微元量,整理得到
\[\begin{split}
\begin{cases}
p_{x} = \sigma_{xx} \, l + \tau_{yx} \, m, \\
p_{y} = \sigma_{yy} \, m + \tau_{xy} \, l.
\end{cases}
\end{split}\]
这表明,只需知道过点 \(P\) 的平行于 \(x\) 轴和 \(y\) 轴的截面上的应力,就能够计算出任意取向截面上的应力
Note
柯西应力定理:在二/三维情况下,任意取向截面上的应力可以通过任意两/三个不平行截面上的应力计算出
将上式写为矩阵形式
(45)\[\begin{split}
\mathbf{p} = \begin{bmatrix}
p_{x}\\
p_{y}
\end{bmatrix}= \begin{bmatrix}
\sigma_{xx} & \tau_{yx} \\
\tau_{xy} & \sigma_{yy}
\end{bmatrix}
\begin{bmatrix}
l \\
m
\end{bmatrix},
\end{split}\]
其中
\[\begin{split}
\boldsymbol{\sigma}=\begin{bmatrix}
\sigma_{xx} & \tau_{yx} \\
\tau_{xy} & \sigma_{yy}
\end{bmatrix}
\end{split}\]
被称为应力张量
\(\overline{AB}\) 上的正应力 \(\sigma_{n}\) 和切应力 \(\tau_{n}\) 分别为
(46)\[\begin{split}
\begin{align*}
\sigma_{n} &= \mathbf{p}\cdot\mathbf{n}=l^{2}\sigma_{xx} + m^{2}\sigma_{yy}+2lm\tau_{xy}=\mathbf{n}^{T}\boldsymbol{\sigma}\mathbf{n},\\
\tau_{n} &= lp_{y}-mp_{x}=lm(\sigma_{yy} - \sigma_{xx})+(l^2-m^2)\tau_{xy}=(\mathbf{n}^\perp)^{T}\boldsymbol{\sigma}\mathbf{n}.
\end{align*}
\end{split}\]
最大正应力和最大切应力
实际工程中通常关注最大正应力和最大切应力,因为它们分别反映了材料在拉伸/压缩和剪切方向上的极限受力状态
最大正应力
由于 \(\boldsymbol{\sigma}\) 是一个实对称矩阵,因此对于任意 \(\mathbf{n}\) 满足
\[
\sigma_2 \leq \mathbf{n}^{T}\boldsymbol{\sigma}\mathbf{n} \leq \sigma_1,
\]
其中,\(\sigma_{1}\geq \sigma_{2}\) 为应力张量 \(\boldsymbol{\sigma}\) 的特征值。这表明,在点 \(P\) 处的最大正应力等于 \(\boldsymbol{\sigma}\) 的最大特征值 \(\sigma_{1}\)。记 \(\sigma_{1}\) 对应的单位特征向量为 \(\mathbf{n}_{1}\),此时有
\[
\mathbf{p} = \boldsymbol{\sigma}\mathbf{n}_{1} = \sigma_{1}\mathbf{n}_{1},
\]
因此,单位法向量为 \(\mathbf{n}_{1}\) 的选取截面上的应力大小与 \(\sigma_{1}\) 相同,方向为截面法方向,这表明此时切应力为 0
将切应力为 0 的截面称为主应力面,主应力面上的正应力被称为主应力,主应力面的法向方向被称为主应力方向。容易知道,点 \(P\) 处的主应力大小就是应力张量 \(\boldsymbol{\sigma}\) 的特征值,方向与对应的特征向量相同
此外,由于 \(\boldsymbol{\sigma}\) 是实对称矩阵,因此其特征值所对应的特征向量是正交的,即主应力相互正交
如果将 \(x\) 轴和 \(y\) 轴分别选定为两个主应力方向,则在该坐标系下,应力张量表示为一个对角矩阵
\[\begin{split}
\boldsymbol{\sigma}=\begin{bmatrix}
\sigma_{1} & 0 \\
0 & \sigma_{2}
\end{bmatrix}.
\end{split}\]
基变换与张量变换
将张量视为一个将任意截面法向量映射为作用在该截面上的应力的线性算子,则在不同的基选择下,应力张量的矩阵表示是相似的
最大切应力
将 \(x\) 轴和 \(y\) 轴分别选定为两个主应力方向,此时,根据切应力计算公式 (46),有
\[
\tau_{n} = lm(\sigma_{2} - \sigma_{1}),
\]
代入 \(l^2 + m^2 = 1\) 消去 \(m\),得到
\[
\tau_n = \pm \sqrt{\frac{1}{4} - \left(\frac{1}{2} - l^2\right)^2} \, (\sigma_2 - \sigma_1),
\]
当 \( \frac{1}{2} - l^2 = 0 \) 时,切应力 \( \tau_n \) 取得最大值,为 \(\tau_{n} = \frac{1}{2} (\sigma_1 - \sigma_2)\),
此时对应截面的法向量与主应力面之间的夹角为 \( 45^\circ \),此时正应力为 \(\sigma_{n} = \frac{1}{2} (\sigma_1 + \sigma_2)\)