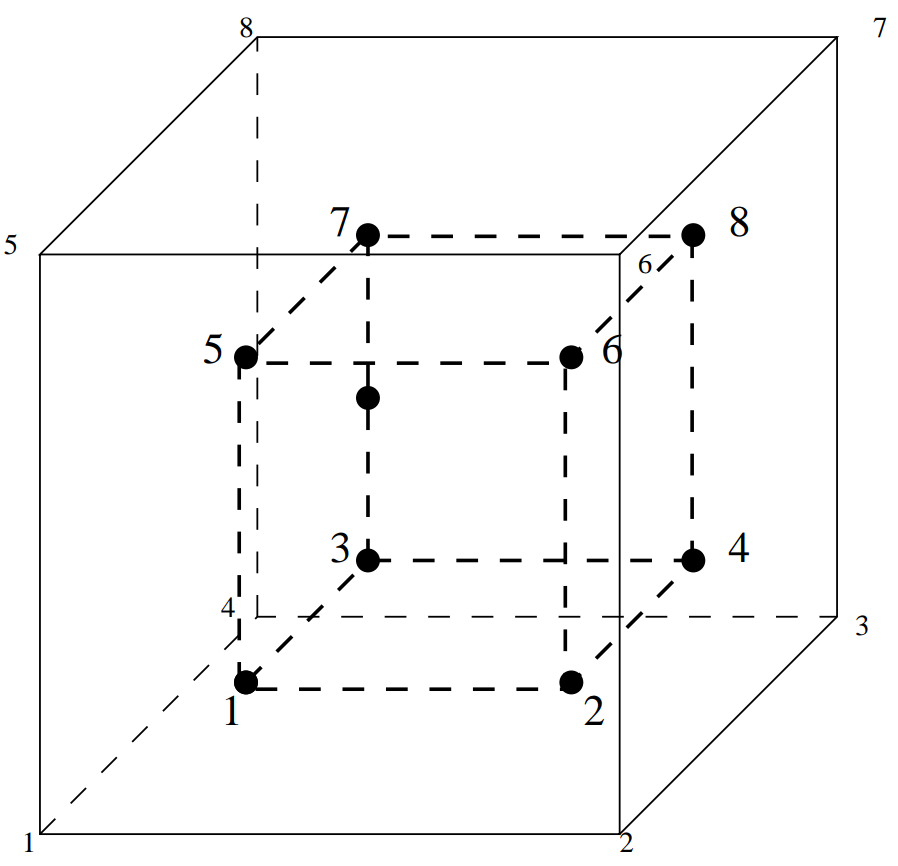
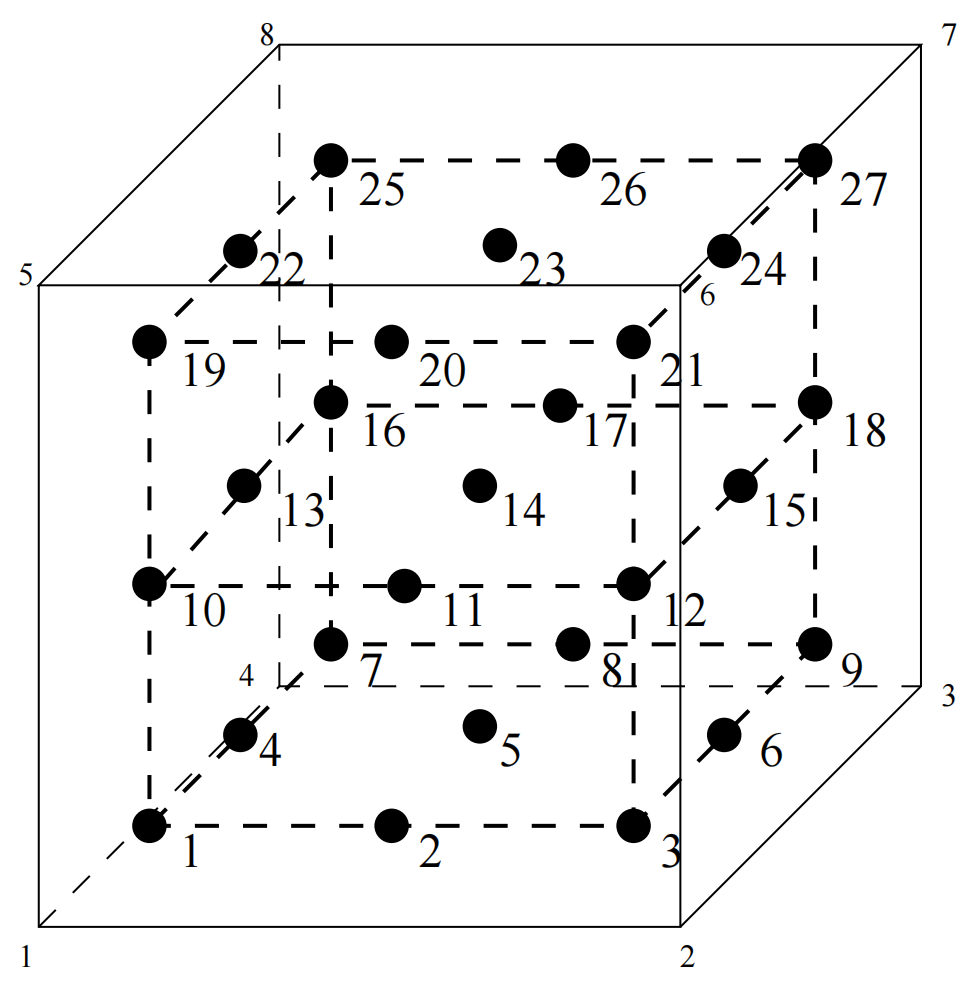
六面体单元

六面体单元#

C3D8#

../../../_images/C3D8.png

Fig. 44 六面体线性单元#

../../../_images/C3D8-int.png

Fig. 45 全积分—8积分点#

形函数#

\[ \begin{equation} \begin{aligned} N_i(\xi, \eta, \zeta) &= \frac{1}{8}(1+\xi_{i}\xi)(1+\eta_{i}\eta)(1+\zeta_{i}\zeta). \end{aligned} \end{equation} \]

数值积分#

全积分能提升积分的计算精度，但同时也导致了过度的刚度，尤其对于低阶单元（例如线性单元），这类单元对复杂变形模式的描述能力有限。因此，使用全积分通常会引入错误约束，最终导致剪切锁死和体积锁死，故该单元不适用于以下情形：

  1. 体积守恒材料行为‌‌：例如，高泊松比系数（\(\rightarrow0.5\)）的材料或塑性行为

  2. 弯曲行为：如细长梁，薄板的弯曲问题

Zienkiewicz, O.C. and Taylor, R.L., The finite element method. McGraw Hill Book Company (1989).

C3D8R#

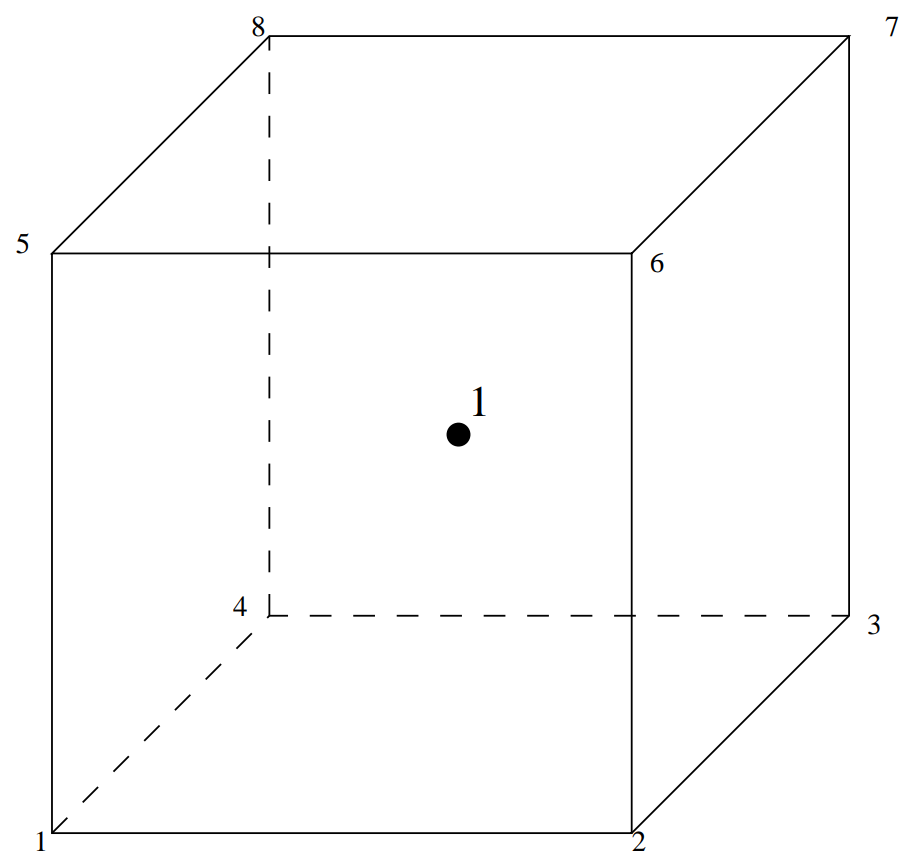
../../../_images/C3D8R-int.png

Fig. 46 六面体线性单元，缩减积分—1积分点#

形函数#

与 C3D8 一致

性能#

该单元在 C3D8 的基础上，使用缩减积分技术（单个积分点），因此显著减轻了死锁现象，在体积守恒和弯曲行为中比 C3D8 表现更好。但同时由于也引入了新的问题

  1. 在弯曲问题中表现不够刚性

  2. 积分点处的应力应变最精确，但由于积分点位于单元中心处，因此在边界处需要使用更小的单元来捕捉应力集中（可视化误差）

  3. 存在 12 个虚假的零能模式导致严重的沙漏效应：这使得位移解被任意大的零能位移叠加，导致完全错误的结果。由于零能模式不会导致任何应力，因此应力场仍然是正确的

实际上，没有沙漏控制，C3D8R 单元并不实用，CCX 自 2.3 版本开始，沙漏控制会自动激活

Flanagan, D.P. and Belytschko, T., Uniform strain hexahedron and quadrilateral with orthogonal hourglass control. Int. J. Num. Meth. Eng. 17 ,679-706 (1981).

C3D8I#

C3D8I（Incompatible Modes）单元是C3D8单元的改进版本，通过引入非协调修正，能够消除剪切锁死并显著缓解体积锁死，尤其适用于线性单元在弯曲作用下使用

形函数#

气泡函数#

气泡函数是在单元内部非零、但在所有单元节点处取值为零的函数，例如

\[ {{N}_{b}}(\xi ,\eta ,\zeta )=(1-{{\xi }^{2}})(1-{{\eta }^{2}})(1-{{\zeta }^{2}}), \]

该函数的主要作用是丰富单元内部的位移场，而不影响节点的自由度

非协调修正#

非协调修正是指在标准位移场的基础上，叠加非协调位移模式，从而提升单元内部的位移场表达能力。这样做虽然在单元内部增强了位移场的灵活性，但在单元边界处可能不再严格满足位移的连续性条件

\[ u=\sum_{i=1}^{8}{{{N}_{i}}}{{u}_{i}}+\sum_{j=1}^{m}{{{\alpha }_{j}}}{{N}_{bj}}(\xi ,\eta ,\zeta ), \]

其中，\(m\) 为附加函数（如气泡函数）的数量，\(\alpha_{j}\) 是与之对应的附加自由度。这些附加自由度用于调节气泡函数对位移场的贡献，避免因高阶项引入导致的数值不稳定问题

附加自由度的确定通常通过能量等效、最小二乘法等方法，使修正后的位移场更好地逼近真实变形模式，其具体实现与单元的几何形状和材料属性相关。例如，\(\alpha_{j}\) 可以通过静力凝聚法（static condensation）或类似的消元方法，在单元层面进行消除，因此不会作为全局自由度参与整体方程组的求解

弱连续性要求：非协调单元允许位移场在单元边界处不连续，需要通过 B-bar ‌方法或稳定化技术等保证收敛

C3D8I 通过引入附加高阶位移函数‌和‌应变场分离技术对位移场进行非协调修正，在保持一阶单元计算效率的同时，显著提升对弯曲、剪切及不可压缩问题的分析精度。其核心在于牺牲局部位移连续性，换取应变场描述的灵活性，从而克服传统线性单元的固有缺陷

尽管 C3D8I 单元的质量远优于 C3D8 单元，并在网格形状较好时精度接近二次单元，但通常使用二次单元（C3D20 和 C3D20R）获得最佳结果

Taylor, R.L, Beresford, P.J. and Wilson, E.L., A non-conforming element for stress analysis. Int. J. Num. Meth. Engng. 10 , 1211-1219 (1976).

C3D20#

../../../_images/C3D20.png

Fig. 47 六面体二次单元#

../../../_images/C3D20-int.png

Fig. 48 全积分—27积分点#

形函数#

角节点#

\[ N_i(\xi, \eta, \zeta) = \frac{1}{8}(1 + \xi \xi_i)(1 + \eta \eta_i)(1 + \zeta \zeta_i)(\xi \xi_i + \eta \eta_i + \zeta \zeta_i - 2) \]

边中点节点#

若该节点在 \(\xi = 0\)，\(\eta = \eta_j\)，\(\zeta = \zeta_j\)，则

\[ N_j(\xi, \eta, \zeta) = \frac{1}{4}(1 - \xi^2)(1 + \eta \eta_j)(1 + \zeta \zeta_j) \]

若该节点在 \(\eta = 0\)，\(\xi = \xi_j\)，\(\zeta = \zeta_j\)，则

\[ N_j(\xi, \eta, \zeta) = \frac{1}{4}(1 + \xi \xi_j)(1 - \eta^2)(1 + \zeta \zeta_j) \]

若该节点在 \(\zeta = 0\)，\(\xi = \xi_j\)，\(\eta = \eta_j\)，则

\[ N_j(\xi, \eta, \zeta) = \frac{1}{4}(1 + \xi \xi_j)(1 + \eta \eta_j)(1 - \zeta^2) \]

性能#

该单元在进行线弹性分析时表现优异，凭借其积分点的合理分布，能够有效捕捉结构表面的应力集中。但在非线性分析中，尽管其缺陷较 C3D8 单元有所减轻，仍不可避免地出现了类似的问题

  • 在等容行为中，全积分表现不佳

  • 在弯曲行为中，表现出过度刚度

L. Lapidus and G. F. Pinder, Numerical Solution of Partial Differential Equations in Science and Engineering. New York: John Wiley & Sons, 1982.

C3D20R#

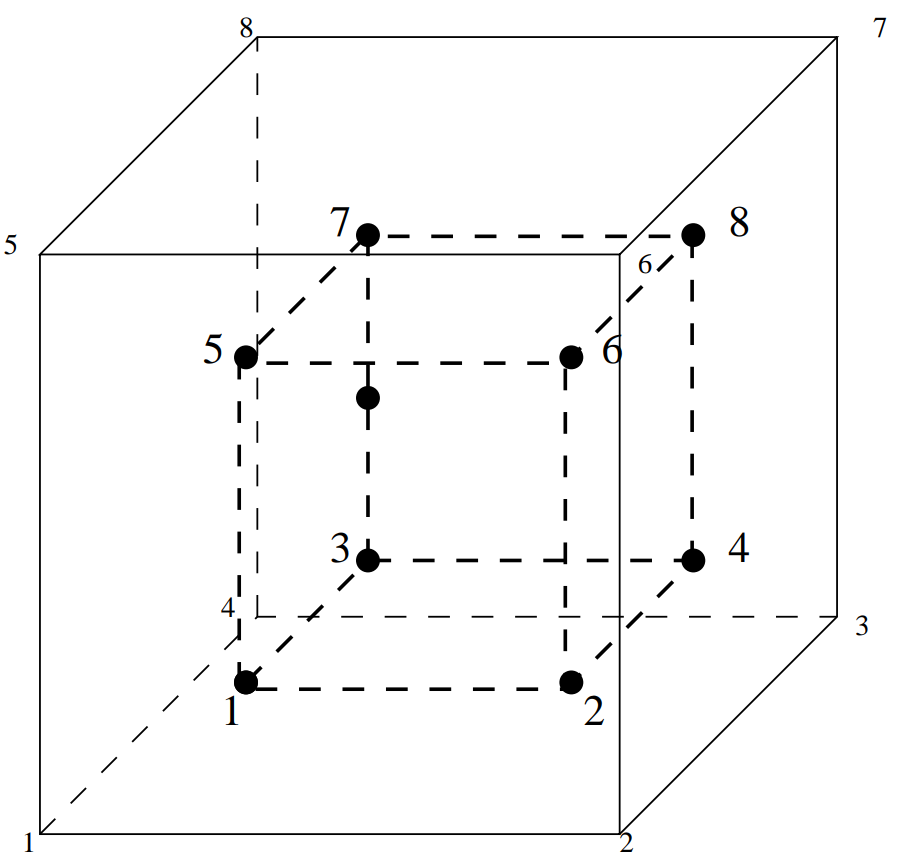
../../../_images/C3D20R-int.png

Fig. 49 六面体二次单元，缩减积分—8积分点#

性能#

该单元性能优异，是一种极具通用性的理想单元

  • 在等容材料行为的模拟中表现出色，在弯曲问题中同样具有良好的适应性

  • 虽然采用了较少的积分点，但极少出现沙漏效应（通常情况下，积分点数量不足会引发虚假模态，导致离散位移场异常，但应力场依然准确）

  • 虽然积分点数量减少，但由于这些点正好选在了有限元解最为精确的超收敛点上，所以得到的刚度矩阵和载荷依然能获得很高的精度

使用该单元时需要注意两点

  • 接触问题：所有二次单元都会在点-面接触计算中引起问题。这是由于高阶单元的形函数与节-面接触算法的数学不兼容。建议使用面-面接触罚方法和motar接触

  • 可视化误差：积分点距离单元边界约为单元尺寸的四分之一。当网格较粗时，将积分点处的应力外推到有限元节点会引入较大的误差，难以准确捕捉结构表面存在的高应力集中现象

J. Barlow, “Optimal stress locations in finite element models,” International Journal for Numerical Methods in Engineering, vol. 10, pp. 243-251, 1976.

Contents