应力 应变 位移

应力、应变和位移是弹性力学中的基本物理量，它们共同揭示了材料在外力作用下的力学行为。应力描述了材料内部的力分布状态，应变反映了材料的变形程度，而位移则刻画了材料各点因受力而产生的位置变化。这三者通过平衡方程、几何方程和本构方程紧密联系，构成了弹性力学分析的核心框架

当物体受到外部作用时，其内部的受力状态、几何形状以及空间位置可能会发生变化。这些变化分别对应于应力、应变和位移的概念：

1. 应力：描述物体内部的受力状态，反映材料在外力作用下抵抗变形或破坏的能力。应力是研究物体强度和稳定性的核心指标

2. 应变：描述物体几何形状的变化，表示物体在受力后形变的程度。应变是衡量材料在外力作用下变形特性的关键参数

3. 位移：描述物体空间位置的变化，指物体在受力作用下，各点从初始位置移动到新位置的过程。位移是研究物体运动和变形行为的基础参数

应力

作用在物体上的力通常可以分为体积力和表面力两大类：

1. 体积力：作用在物体整个体积上的力，如重力、电磁力和惯性力，通常由场力引起

2. 表面力：作用在物体表面上的力，如压力、摩擦力等，通常由物体与外部环境接触引起

作用于固体表面的力通过表层分子依靠分子间的相互作用力向各个方向传递，最终影响固体内部任意一点的受力状态。固体内部由于分子间相互作用而产生的力被称为内力

借助微观结构，有助于深入地理解固体的力学性质。例如，为什么某一点会受到来自各个方向的应力？为什么一个方向的外力会引起另一个方向的形变？

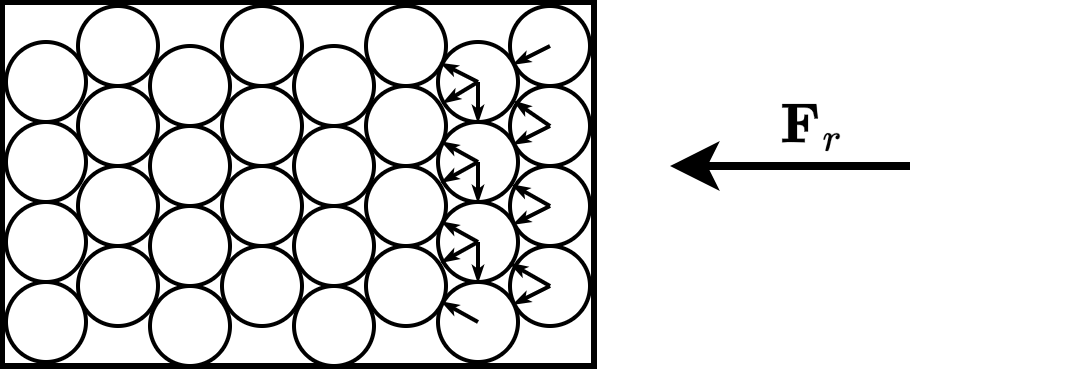
Fig. 24 表面力通过分子间的相互作用力向各个方向传递

为了研究物体内部某一点 \(P\) 处的内力，通过 \(P\) 点作一个截面 \(R\)，将物体分为 \(I\) 和 \(II\) 两个部分。在截面 \(R\) 上，部分 \(I\) 对部分 \(II\) 施加作用力

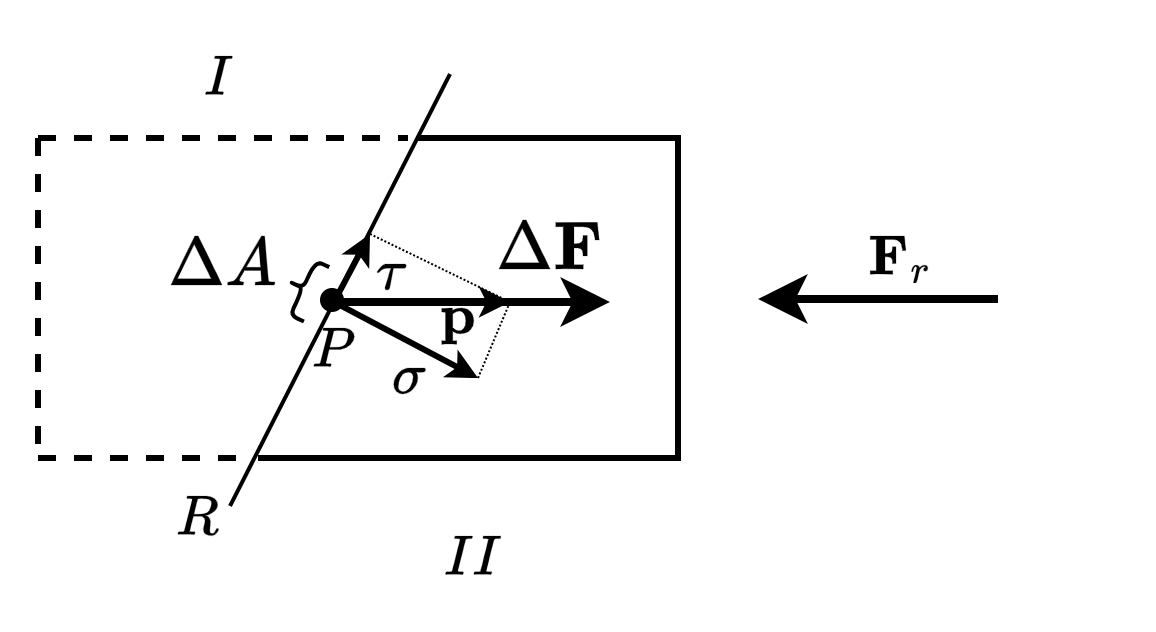
Fig. 25 通过截面法暴露内力

截面的法向量为常量；\(\Delta \mathbf{F}\) 是矢量，且随空间位置变化

取截面 \(R\) 上包含点 \(P\) 的面积为 \(\Delta A\) 上的区域，设作用在该区域上的内力为 \(\Delta \mathbf{F}\)，记 \(\frac{\Delta \mathbf{F}}{\Delta A}\) 为内力的平均集度（平均应力），于是在点 \(P\) 处的应力定义为

应力是单位面积的力

\[ \lim_{\Delta A \to 0} \frac{\Delta \mathbf{F}}{\Delta A} = \mathbf{p} \]

若 \(\Delta A\) 是变形前的面积，则 \(\mathbf{P}\) 被称为工程应力

\(\mathbf{P}\) 称为 Cauchy 应力，也称真实应力，直接反映了物体在当前状态下受力情况

应力可以分解为沿其作用截面的法线方向的分量和切向方向的分量，分别称为正应力 \(\sigma\) 和切应力 \(\tau\)。这两个分量与物体的形变行为及材料的强度密切相关

应变

假设物体发生变形后，点 \(A\) 和点 \(B\) 分别移动到了 \(A^{'}\) 和 \(B^{'}\)。由此，线段（例如，\(\overline{PA},\overline{PB}\)）的长度发生了伸缩变化，它们的夹角也发生改变

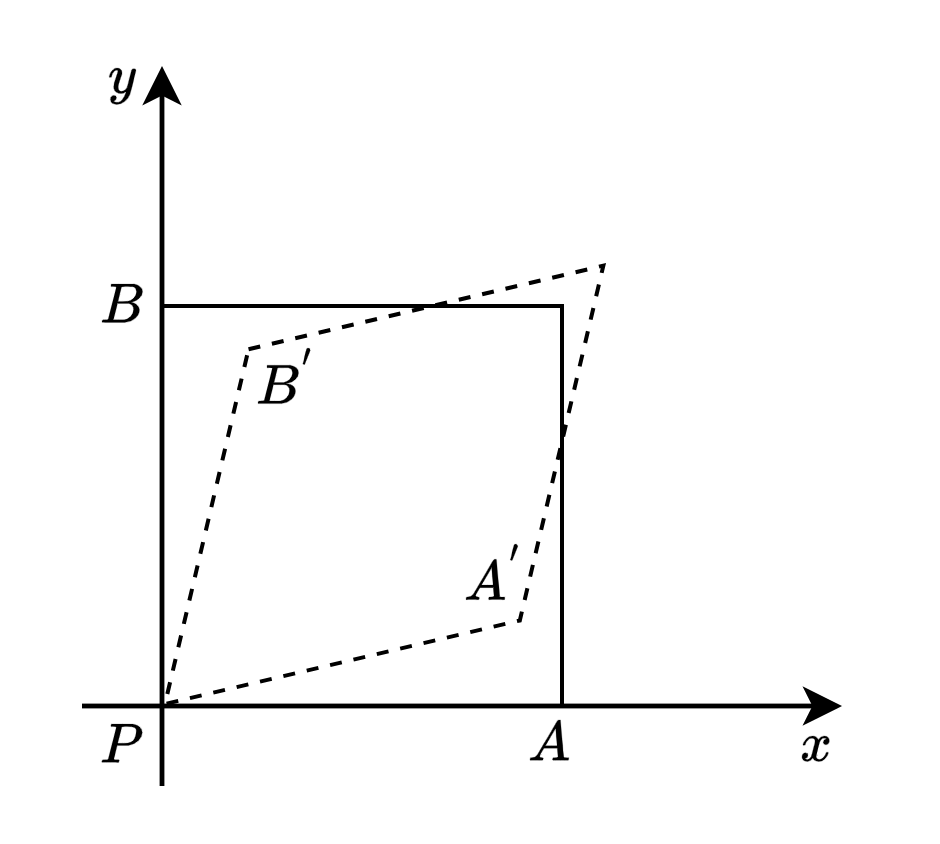
Fig. 26 形变可以总结为长度与角度的改变

线应变是无量纲量，以伸长为正
切应变的单位是弧度，以直角角度变小为正

1. 线应变：也称正应变，表示物体单位长度的伸缩变化

2. 切应变：表示由直角夹角发生的改变，用于描述形状的剪切变形程度

位移

位移描述了物体中各点空间位置的变化。点与点之间的相对位移决定了物体的形变状态，因为形变的本质是由不同点之间的位置变化差异所引起的

Note

应变描述了相对位置的变化，位移反映了绝对位置的变化

当物体中各个点的位移均为 \(\mathbf{0}\) 时，物体一定没有发生形变；然而，当物体未发生形变时，各个点的位移未必为 \(\mathbf{0}\)。例如，在刚体运动的情况下，物体可能整体发生平移或旋转