Mohr 圆
莫尔圆(Mohr’s circle)是一种以图形方式表示二维柯西应力张量在不同取向平面上分量变化关系的工具。通过莫尔圆,可以直观地确定同一点上任意取向平面上的正应力和切应力分量,以及主应力和极值剪切应力

Fig. 41 一般三维应力下的莫尔圆
假设主应力 \(\sigma_{1}> \sigma_{2}> \sigma_{3}\),对应的单位特征向量为 \(\mathbf{n}_{1},\mathbf{n}_{2},\mathbf{n}_{3}\),设截面法向量为
\[
\mathbf{n} = n_{1}\mathbf{n}_{1} + n_{2}\mathbf{n}_{2} + n_{2}\mathbf{n}_{2},
\]
其中
(92)\[
1 = n_{1}^{2}+n_{2}^{2}+n_{3}^{2},
\]
于是
(93)\[\begin{split}
\begin{equation}
\begin{aligned}
\sigma_{\mathbf{n}} &= \mathbf{n}^{T}\boldsymbol{\sigma}\mathbf{n} = n_{1}^{2}\sigma_{1} + n_{2}^{2}\sigma_{2} + n_{3}^{2}\sigma_{3},\\
\tau_{\mathbf{n}}^{2} + \sigma_{\mathbf{n}}^{2} &= \mathbf{n}^{T}\boldsymbol{\sigma}^{2}\mathbf{n} = n_{1}^{2}\sigma_{1}^{2} + n_{2}^{2}\sigma_{2}^{2} + n_{3}^{2}\sigma_{3}^{2}.
\end{aligned}
\end{equation}
\end{split}\]
使用克拉默法则求解线性方程组 (92) 和 (93),得到
(94)\[\begin{split}
\begin{equation}
\begin{aligned}
n_1^2 &= \frac{\tau_{\mathbf{n}}^2 + (\sigma_{\mathbf{n}} - \sigma_2)(\sigma_{\mathbf{n}} - \sigma_3)}{(\sigma_1 - \sigma_2)(\sigma_1 - \sigma_3)} \geq 0,\\
n_2^2 &= \frac{\tau_{\mathbf{n}}^2 + (\sigma_{\mathbf{n}} - \sigma_3)(\sigma_{\mathbf{n}} - \sigma_1)}{(\sigma_2 - \sigma_3)(\sigma_2 - \sigma_1)} \geq 0,\\
n_3^2 &= \frac{\tau_{\mathbf{n}}^2 + (\sigma_{\mathbf{n}} - \sigma_1)(\sigma_{\mathbf{n}} - \sigma_2)}{(\sigma_3 - \sigma_1)(\sigma_3 - \sigma_2)} \geq 0,
\end{aligned}
\end{equation}
\end{split}\]
由于 \(\sigma_{1}>\sigma_{2}>\sigma_{3}\),于是将上述方程整理得到
(95)\[\begin{split}
\begin{equation}
\begin{aligned}
&\tau_{\mathbf{n}}^2 + \left[\sigma_{\mathbf{n}} - \frac{1}{2}(\sigma_2 + \sigma_3)\right]^2 \geq \left(\frac{1}{2}(\sigma_2 - \sigma_3)\right)^2,\\
&\tau_{\mathbf{n}}^2 + \left[\sigma_{\mathbf{n}} - \frac{1}{2}(\sigma_1 + \sigma_3)\right]^2 \leq \left(\frac{1}{2}(\sigma_1 - \sigma_3)\right)^2,\\
&\tau_{\mathbf{n}}^2 + \left[\sigma_{\mathbf{n}} - \frac{1}{2}(\sigma_1 + \sigma_2)\right]^2 \geq \left(\frac{1}{2}(\sigma_1 - \sigma_2)\right)^2,
\end{aligned}
\end{equation}
\end{split}\]
根据上述关系式,可以得到,所有截面的切应力和正应力都落在了图 Fig. 41 中的绿色部分
Mohr–Coulomb 屈服准则
对于岩石、土壤等土体以及混凝土等材料,非弹性变形通常由剪切面上的滑移或摩擦主导。在这些材料中,破坏发生的面满足
\[
\tau_{\mathbf{n}} \geq c - \tan\phi\cdot\sigma_{\mathbf{n}},
\]
其中,\(\tau_{f}=-\tan\phi\cdot\sigma_{\mathbf{n}}\) 是摩擦强度项,\(\phi\) 为内摩擦角,\(c\) 是材料的粘聚力
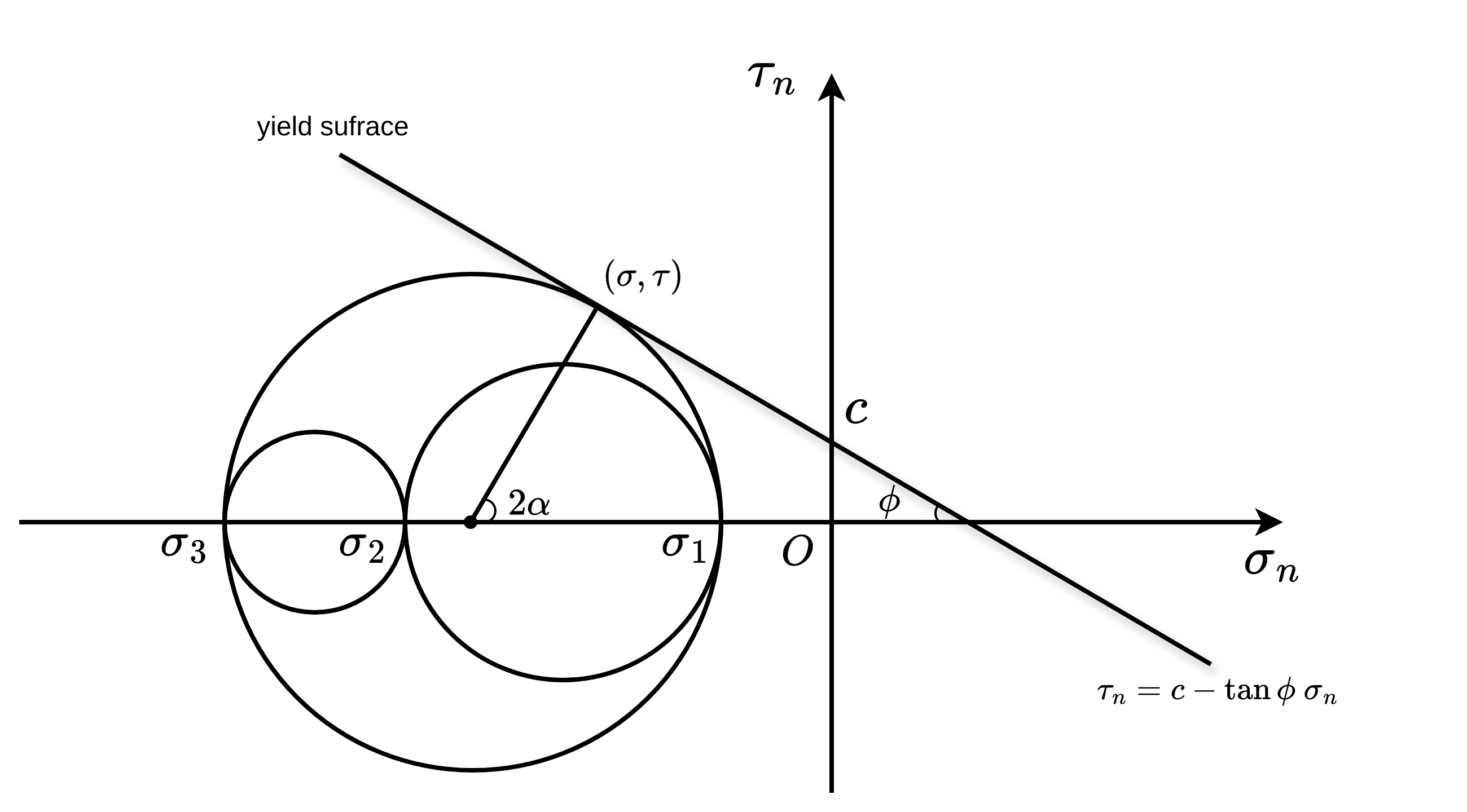
Fig. 42 屈服点位于 Morh 圆与直线 \(\tau_{\mathbf{n}} = c - \tan\phi\cdot\sigma_{\mathbf{n}}\) 的相切处
如上图所示,随着应力状态的演化,屈服发生在 Morh 圆与直线 \(\tau_{\mathbf{n}} = c - \tan\phi\cdot\sigma_{\mathbf{n}}\) 的相切处,此时 \(2\alpha = \frac{\pi}{2}-\phi\),过点 \((\frac{\sigma_{1}+\sigma_{3}}{2},0)\),斜率为 \(\tan2\alpha\) 作直线,与 Morh 圆交于
\[\begin{split}
\begin{equation}
\begin{aligned}
\sigma_{\mathbf{n}} &= \frac{\sigma_1 + \sigma_3}{2} + \frac{\sigma_1 - \sigma_3}{2} \cos 2\alpha, \\
\tau_{\mathbf{n}} &= \frac{\sigma_1 - \sigma_3}{2} \sin 2\alpha,
\end{aligned}
\end{equation}
\end{split}\]
由于直线 \(\tau_{\mathbf{n}} = c - \tan\phi\cdot\sigma_{\mathbf{n}}\) 经过该点,因此
\[
\frac{\sigma_1 - \sigma_3}{2} \cos \phi = c - \tan\phi\cdot(\frac{\sigma_1 + \sigma_3}{2} + \frac{\sigma_1 - \sigma_3}{2} \sin \phi),
\]
整理得到 Mohr–Coulomb 屈服准则
\[
(\sigma_1 - \sigma_3) + (\sigma_1 + \sigma_3)\sin\phi=2c\cos\phi,
\]
或
\[
(\sigma_{\max} - \sigma_{\min}) + (\sigma_{\max} + \sigma_{\min})\sin\phi=2c\cos\phi,
\]
不变量形式
\[
\frac{1}{3} I_1 \sin \phi
+ \left( \cos \theta - \frac{1}{\sqrt{3}} \sin \theta \sin \phi \right) \sqrt{J_2}
- c \cos \phi = 0,
\]
其中,\(\theta\) 是 Lode 角
\[
\sin 3\theta = \pm\frac{3\sqrt{3}}{2} \frac{J_3}{J_2^{3/2}}.
\]
如果取拉应力为正(\(\sigma_{1}\geq\sigma_{2}\geq\sigma_{3}\)),则取正号


