平面应力问题
下图展示了等厚薄板的受力情况,其中厚度远小于板的长度与宽度
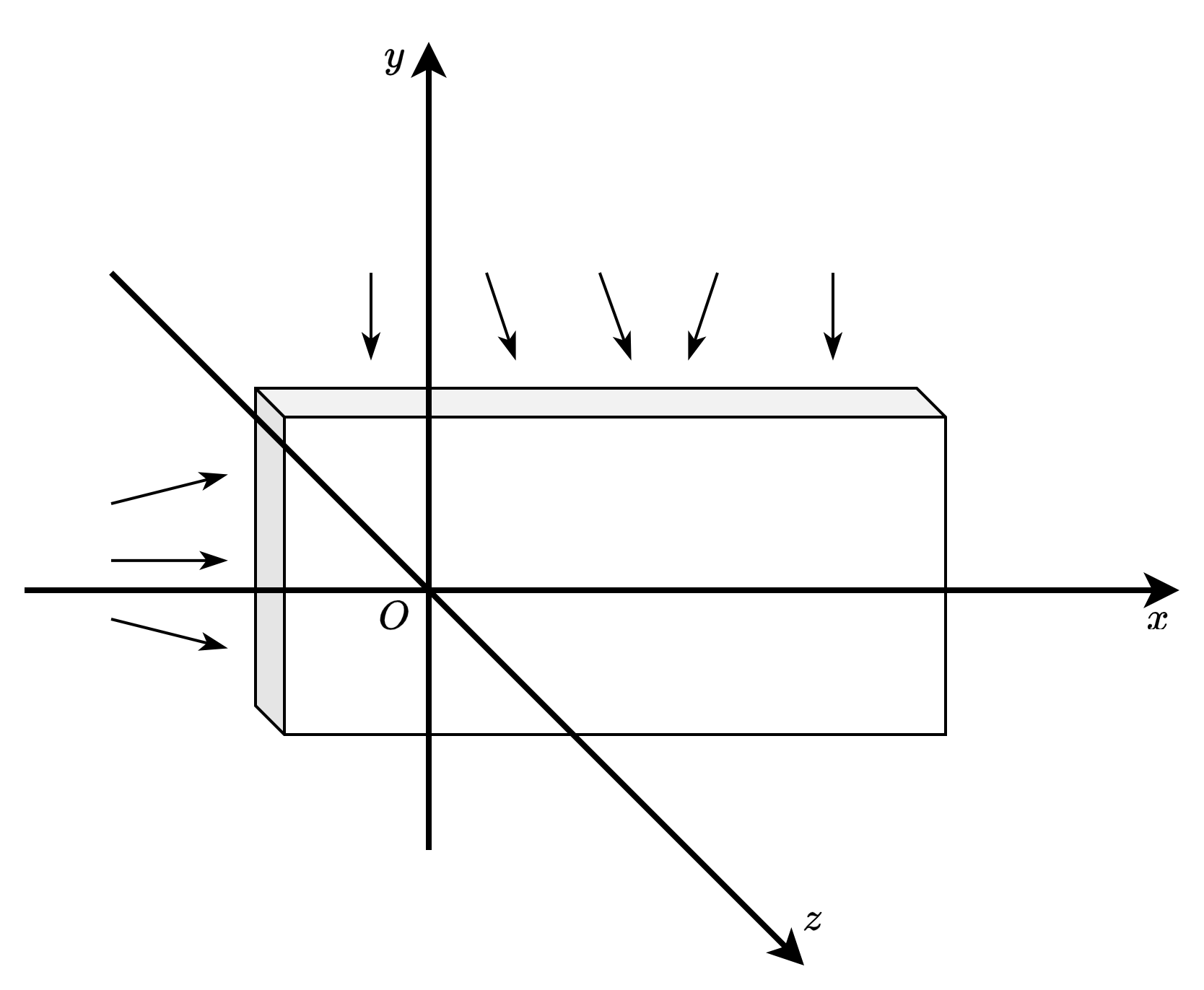
Fig. 30 等厚薄板的受力情况
薄板仅在边缘的 \(x\) 轴截面和 \(y\) 轴截面上受到不随厚度变化的外力,而在边缘的 \(z\) 轴截面上无外力作用。由于薄板足够薄,因此在薄板内的任意一点都满足
\[
\sigma_{zz}=0,\quad \sigma_{zx} = 0,\quad \sigma_{zy} = 0.
\]
此外,由切应力互等定理,有
\[
\sigma_{xz} = 0,\quad \sigma_{yz} = 0.
\]
因此,\(\gamma_{zx} = \gamma_{zy} = 0\)
由于薄板很薄,且作用力不随厚度变化,因此可以认为应力分量 \(\sigma_{xx},\sigma_{yy}, \sigma_{xy}\) 和应变分量 \(\varepsilon_{xx},\varepsilon_{yy}, \gamma_{xy}\) 是关于 \(x\) 和 \(y\) 的函数,不随 \(z\) 变化
这类问题被称为平面应力问题,
此时,方程 (48) 可简化为
(50)\[\begin{split}
\begin{equation}
\begin{aligned}
&\varepsilon_{xx} = \frac{1}{E} ( \sigma_{xx} - \nu \sigma_{yy} ),\\
&\varepsilon_{yy} = \frac{1}{E} (\sigma_{yy} - \nu \sigma_{xx} ),\\
&\gamma_{xy} = \frac{2(1+\nu)}{E} \sigma_{xy}.
\end{aligned}
\end{equation}
\end{split}\]
\(\varepsilon_{zz}\) 可通过 \(\varepsilon_{zz}=-\frac{\nu}{E} (\sigma_{xx} + \sigma_{yy})\) 求得
Note
物质的宏观形变源于微观分子结构及分子间作用力的耦合效应。因此,即使某方向无外力作用,内部应力传递仍可能导致该方向形变。
在平面应力问题中,所求解的方程组是
(51)\[\begin{split}
\begin{equation}
\begin{aligned}
&\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \sigma_{yx}}{\partial y} + f_x = 0, \\
&\frac{\partial \sigma_{yy}}{\partial y} + \frac{\partial \sigma_{xy}}{\partial x} + f_y = 0,\\
&\varepsilon_{xx} = \frac{\partial u}{\partial x}, \\
&\varepsilon_{yy} = \frac{\partial v}{\partial y}, \\
&\gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y},\\
&\varepsilon_{xx} = \frac{1}{E} ( \sigma_{xx} - \nu \sigma_{yy} ),\\
&\varepsilon_{yy} = \frac{1}{E} (\sigma_{yy} - \nu \sigma_{xx} ),\\
&\gamma_{xy} = \frac{2(1+\nu)}{E} \sigma_{xy},
\end{aligned}
\end{equation}
\end{split}\]
求解变量为
\[
\sigma_{xx}, \, \sigma_{yy}, \, \sigma_{xy}, \, \varepsilon_{xx}, \, \varepsilon_{yy}, \, \gamma_{xy}, \, u, \, v
\]
平面应变问题
假设有无限长的等截面柱形体,柱面上受有平行于 \(z\) 轴截面且不随长度变化的力(面力、体力)或约束
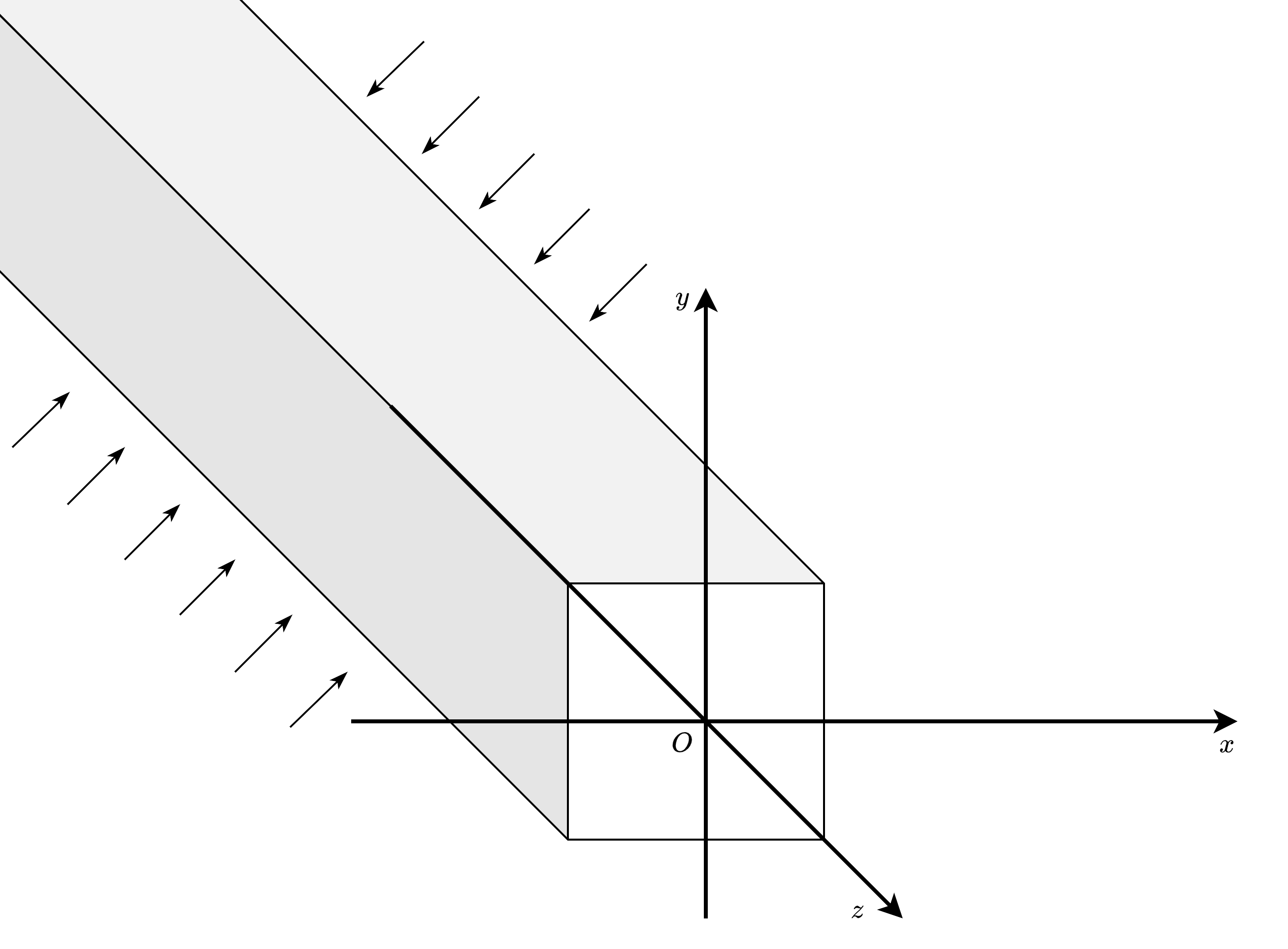
Fig. 31 等截面柱形体的受力情况
假设柱体无限长,则任意 \(z\) 轴截面上的应力、应变和位移分量均不随 \(z\) 方向变化,仅为 \(x\) 和 \(y\) 的函数。
此外,由于对称性,位移仅沿 \(x\) 和 \(y\) 方向发生,且 \(z\) 轴截面上各点的切应力均为 0,因此
\[
\varepsilon_{zz} = 0,\quad \sigma_{zx} = 0,\quad \sigma_{zy}=0.
\]
由胡克定律(见(48)),有
\[
\gamma_{zx} = 0,\quad \gamma_{zy} = 0.
\]
代入 \(\sigma_{zz}=\nu(\sigma_{xx} + \sigma_{yy})\) 消去 \(\sigma_{zz}\),方程 (48) 可简化为
(52)\[\begin{split}
\begin{equation}
\begin{aligned}
&\varepsilon_x = \frac{1 - \nu^2}{E} \left( \sigma_{xx} - \frac{\nu}{1 - \nu} \sigma_{yy} \right), \\
&\varepsilon_y = \frac{1 - \nu^2}{E} \left( \sigma_{yy} - \frac{\nu}{1 - \nu} \sigma_{xx} \right), \\
&\gamma_{xy} = \frac{2(1 + \nu)}{E} \sigma_{xy}.
\end{aligned}
\end{equation}
\end{split}\]
在平面应变问题中,所求解的方程组是
(53)\[\begin{split}
\begin{equation}
\begin{aligned}
&\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \sigma_{yx}}{\partial y} + f_x = 0, \\
&\frac{\partial \sigma_{yy}}{\partial y} + \frac{\partial \sigma_{xy}}{\partial x} + f_y = 0,\\
&\varepsilon_{xx} = \frac{\partial u}{\partial x}, \\
&\varepsilon_{yy} = \frac{\partial v}{\partial y}, \\
&\gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y},\\
&\varepsilon_x = \frac{1 - \nu^2}{E} \left( \sigma_{xx} - \frac{\nu}{1 - \nu} \sigma_{yy} \right), \\
&\varepsilon_y = \frac{1 - \nu^2}{E} \left( \sigma_{yy} - \frac{\nu}{1 - \nu} \sigma_{xx} \right), \\
&\gamma_{xy} = \frac{2(1 + \nu)}{E} \sigma_{xy},
\end{aligned}
\end{equation}
\end{split}\]
求解变量为
\[
\sigma_{xx}, \, \sigma_{yy}, \, \sigma_{xy}, \, \varepsilon_{xx}, \, \varepsilon_{yy}, \, \gamma_{xy}, \, u, \, v
\]
Note
在平面应力问题的方程 (50) 中,如果将 \(E\) 和 \(\nu\) 分别替换为
\[
\frac{E}{1-\nu^2},\quad \frac{\nu}{1-\nu}
\]
就能够得到平面应变问题。如果已经得到平面应力问题的(解析)解,只需将 \(E\) 和 \(\nu\) 作同样的转换,就可以得到相应的平面应变问题的解


