边界条件

边界条件#

边界条件用于描述物体在外力、位移或其他约束作用下的边界行为，是决定物体受力后变形和应力分布的关键因素。通常，边界条件分为应力边界条件，位移边界条件和混合边界条件。记边界为 \(\mathcal{B}\)

  • 应力边界条件：

    \[ \begin{equation} \boldsymbol{\sigma}\cdot\mathbf{n}= \mathbf{f}_{b},\quad \text{on}\,\, \mathcal{B}. \end{equation} \]

  • 位移边界条件：

    \[ \mathbf{u} = \mathbf{u}_{b},\quad \text{on}\,\, \mathcal{B}. \]

  • 混合边界条件：

    \[\begin{split} \begin{equation} \begin{aligned} \boldsymbol{\sigma}\cdot\mathbf{n} &= \mathbf{f}_{b},\quad &\text{on}\,\, \mathcal{B}_{1},\\ \mathbf{u} &= \mathbf{u}_{b},\quad &\text{on}\,\, \mathcal{B}_{2}. \end{aligned} \end{equation} \end{split}\]

在求解弹性力学问题时，应力分量、形变分量和位移分量等不仅需要满足区域内的三套基本方程，还必须符合边界上的边界条件。因此，弹性力学问题属于数学物理方程中的边值问题

圣维南原理#

严格满足边界条件通常会遇到较大的困难，而圣维南原理则为简化局部边界上的应力边界条件提供了极大的便利

圣维南原理：静力等效的力分布仅影响局部区域的应力状态，而对整体结构的远场应力分布几乎没有影响

圣维南原理表明：在距离载荷作用区域足够远的地方，载荷的具体分布方式对结构的应力和变形影响可以忽略不计，只需关注载荷的合力及合力矩的作用效果

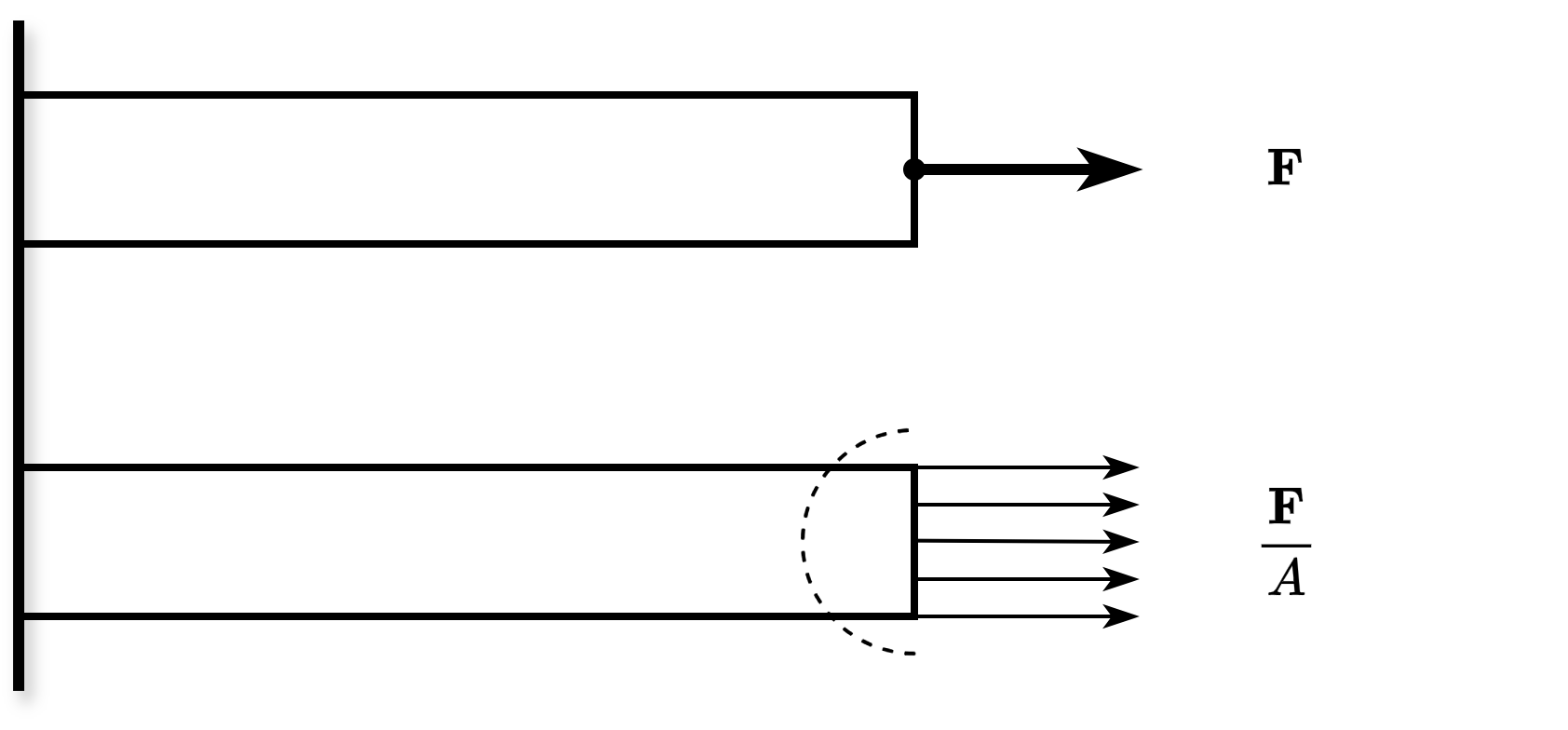
../../../_images/SV-principle.png

Fig. 32 在小边界上进行静力等效变换#

在如图所示的构件中，当将右端截面的拉力替换为均匀分布的拉力（集度为 \(\frac{F}{A}\)）时，根据圣维南原理，只有靠近虚线所示区域的应力分布会发生显著变化，而远离该区域的其余部分受到的影响可以忽略不计

圣维南原理推广

如果物体某一小部分边界上施加的面力是一个平衡力系，那么这种面力的影响仅局限于施力区域附近，在较远处引起的应力可以忽略不计

这表明，平衡力系的影响具有局部性。两个例子：

  • 当没有体力作用时，小孔口边界上的平衡力系仅会在小孔口附近引起局部应力分布

  • 在结构中，开孔与不开孔的情况相比，两者的应力分布仅在孔口附近区域存在显著差异，而远离孔口的区域几乎没有影响

边界条件应用#

假设在局部边界 \(\Gamma\) 上应力需满足

\[ (\boldsymbol{\sigma}\cdot \mathbf{n})|_\Gamma = \mathbf{f} \]

这实际上是一个处处相等的函数方程。然而，这种方程不仅难以求解，而且在实际问题中往往难以严格满足。通过应用圣维南原理，可以将上述条件用静力等效条件替代，即

\[\begin{split} \begin{equation} \begin{aligned} &\int_\Gamma \boldsymbol{\sigma}\cdot \mathbf{n}\, \mathrm{d}\Gamma = \int_\Gamma \mathbf{f}\, \mathrm{d}\Gamma = \mathbf{F},\\ &\int_\Gamma (\boldsymbol{\sigma}\cdot \mathbf{n}) \times \mathbf{r}\, \mathrm{d}\Gamma = \int_\Gamma \mathbf{f}\times \mathbf{r}\, \mathrm{d}\Gamma = \mathbf{M}. \end{aligned} \end{equation} \end{split}\]

上式是一个相对更易求解的积分方程，从而显著简化了问题的求解过程

Contents