几何方程
几何方程揭示了应变与位移之间的内在联系。应变的本质源于不同点之间相对位置的变化。因此,通过分析不同方向上两条线段端点的相对位置变化,可以推导出应变与位移的关系方程
考虑弹性体内任一点 \(P\),沿 \(x\) 轴和 \(y\) 轴的正方向取两个微小线段\(\overline{PA} = \mathrm{d}x \) 和 \(\overline{PA} = \mathrm{d}y\),假定弹性体受力后 \(P,A,B\) 三点分别移动到了 \(P^`,A^`,B^`\)
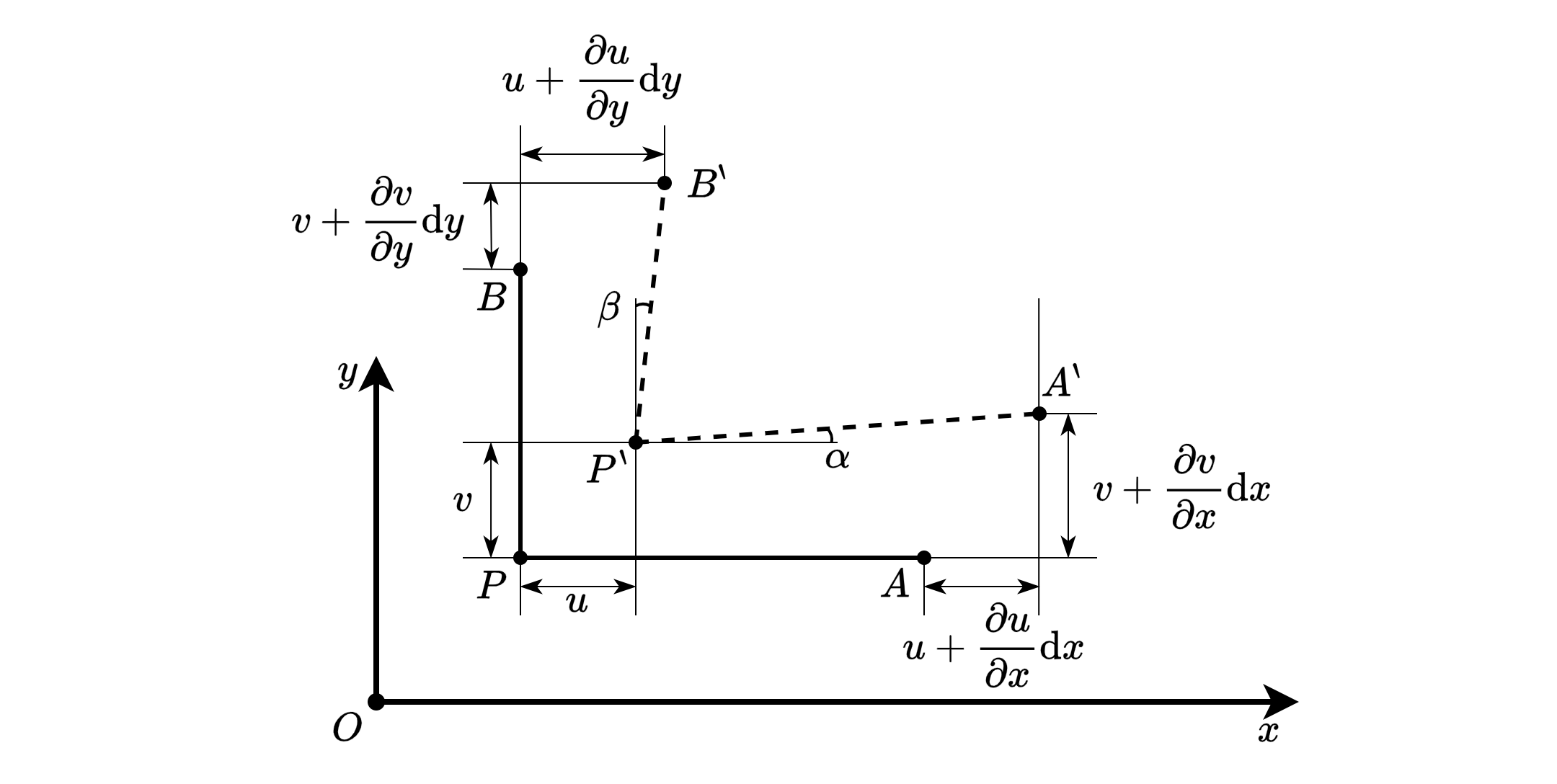
Fig. 29 位移和应变关系示意图
\[\begin{split}
\begin{equation}
\begin{aligned}
u(P)&=u(x_{P},y_{P}),\\
u(A)&=u(x_{A},y_{A})=u(x_{P}+\mathrm{d}x,y_{P}) \approx u(x_{P},y_{P}) + \frac{\partial u}{\partial x}(x_P,y_P)\cdot\mathrm{d}x,\\
u(B)&=u(x_{B},y_{B})=u(x_{P},y_{P}+\mathrm{d}y) \approx u(x_{P},y_{P}) + \frac{\partial u}{\partial y}(x_P,y_P)\cdot\mathrm{d}y,\\
v(P)&=v(x_{P},y_{P}),\\
v(A)&=v(x_{A},y_{A})=v(x_{P}+\mathrm{d}x,y_{P}) \approx v(x_{P},y_{P}) + \frac{\partial v}{\partial x}(x_P,y_P)\cdot\mathrm{d}x,\\
v(B)&=v(x_{B},y_{B})=v(x_{P},y_{P}+\mathrm{d}y) \approx v(x_{P},y_{P}) + \frac{\partial v}{\partial y}(x_P,y_P)\cdot\mathrm{d}y.\\
\end{aligned}
\end{equation}
\end{split}\]
于是,\(\overline{PA}\) 的线应变为
\[
\varepsilon_{xx} = \frac{\left( u + \frac{\partial u}{\partial x} \, \mathrm{d}x \right) - u}{\mathrm{d}x} = \frac{\partial u}{\partial x},
\]
类似地,\(\overline{PB}\) 的线应变为
\[
\varepsilon_{yy} = \frac{\partial v}{\partial y}.
\]
对于 \(\overline{PA}\) 的转角 \(\alpha\) 有
\[
\alpha = \frac{\left( v + \frac{\partial v}{\partial x} \, \mathrm{d}x \right) - v}{\mathrm{d}x} = \frac{\partial v}{\partial x},
\]
类似地,\(\overline{PB}\) 的转角
\[
\beta = \frac{\partial u}{\partial y},
\]
于是切应变 \(\gamma_{xy}\) 为
\[
\gamma_{xy} = \alpha + \beta = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}.
\]
将几何方程整理如下
(47)\[\begin{split}
\begin{equation}
\begin{aligned}
&\varepsilon_{xx} = \frac{\partial u}{\partial x}, \\
&\varepsilon_{yy} = \frac{\partial v}{\partial y}, \\
&\gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}.
\end{aligned}
\end{equation}
\end{split}\]
可以写为
\[
\boldsymbol{\varepsilon} = \frac{1}{2}(\nabla \mathbf{u} + \nabla\mathbf{u}^{T}),
\]
其中,\(\boldsymbol{\varepsilon}\) 是应变张量,\(\mathbf{u} = [u\,v]^{T}\) 是位移向量,即
\[\begin{split}
\begin{equation}
\boldsymbol{\varepsilon}=
\begin{bmatrix}
\varepsilon_{xx} & \varepsilon_{xy} \\
\varepsilon_{yx} & \varepsilon_{yy}
\end{bmatrix} = \frac{1}{2}(\begin{bmatrix}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y}
\end{bmatrix} +
\begin{bmatrix}
\frac{\partial u}{\partial x} & \frac{\partial v}{\partial x} \\
\frac{\partial u}{\partial y} & \frac{\partial v}{\partial y}
\end{bmatrix}),
\end{equation}
\end{split}\]
也可以写为 Voigt 形式
\[\begin{split}
\begin{equation}
\begin{bmatrix}
\varepsilon_{xx} \\ \varepsilon_{yy} \\ 2\varepsilon_{xy}
\end{bmatrix}
=\begin{bmatrix}
\frac{\partial }{\partial x} & 0 \\
0 & \frac{\partial }{\partial y} \\
\frac{\partial }{\partial y} & \frac{\partial }{\partial x}
\end{bmatrix}
\begin{bmatrix}
u \\ v
\end{bmatrix}.
\end{equation}
\end{split}\]
对于三维情形,有
\[\begin{split}
\begin{equation}
\begin{bmatrix}
\varepsilon_{xx}\\\varepsilon_{yy}\\\varepsilon_{zz}\\2\varepsilon_{xy}\\2\varepsilon_{yz}\\2\varepsilon_{zx}
\end{bmatrix}
=\begin{bmatrix}
\frac{\partial}{\partial x} & 0 & 0 \\
0 & \frac{\partial}{\partial y} & 0 \\
0 & 0 & \frac{\partial}{\partial z} \\
\frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0 \\
0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial y} \\
\frac{\partial}{\partial z} & 0 & \frac{\partial}{\partial x}
\end{bmatrix}
\begin{bmatrix}
u_{x}\\u_{y}\\u_{z}
\end{bmatrix}.
\end{equation}
\end{split}\]
刚体运动
当位移分量 \(u,v\) 完全确定时,应变分量 \(\varepsilon_{xx}, \varepsilon_{yy}, \gamma_{xy}\) 也完全确定。反之,应变分量完全确定时,位移分量不能完全确定。
假设
\[
\varepsilon_{xx} = \varepsilon_{yy} = \gamma_{xy} = 0,
\]
则
\[
\frac{\partial u}{\partial x} = 0, \quad
\frac{\partial v}{\partial y} = 0, \quad
\gamma_{xy} = 0,
\]
可得
\[
u = u_{0} - wy,\quad
v = v_{0} + wx.
\]
\(u_{0}\) 和 \(v_{0}\) 分别表示物体沿 \(x\) 轴和 \(y\) 轴方向的刚体平移,而 \(w\) 则为物体绕 \(z\) 轴的刚体转动。当只有 \(w\) 不为 0 时,对于坐标内任一点 \(P\),其位移分量为 \(u=-wy, v = wx\),满足
\[\begin{split}
\begin{bmatrix}
u & v
\end{bmatrix}
\begin{bmatrix}
x \\ y
\end{bmatrix} = 0,
\end{split}\]
因此,点 \(P\) 的位移方向为以原点 \(O\) 为圆心,\(\overline{OP}\) 为半径的圆在 \(P\) 点的切向。由于位移是微小的(\(w\)非常小),因此运动表现为刚体转动,位移为
\[
\sqrt{u^2+v^2}=w\sqrt{x^2+y^2}.
\]